2015年全国统一高考文科数学试卷(全国Ⅰ卷)
如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从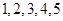 中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
| A. | B. | C. | D. |
已知椭圆E的中心为坐标原点,离心率为 , 的右焦点与抛物线 的焦点重合, 是 的准线与E的两个交点,则 ()
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:"今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?"其意思为:"在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?"已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )
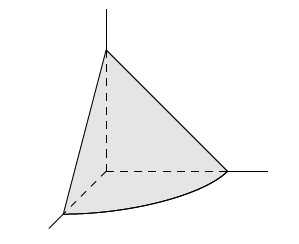
| A. | 14斛 | B. | 22斛 | C. | 36斛 | D. | 66斛 |
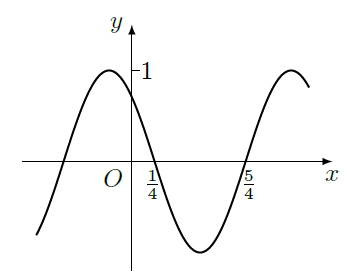
圆柱被一个平面截去一部分后与半球(半径为
)组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为
,则
( )
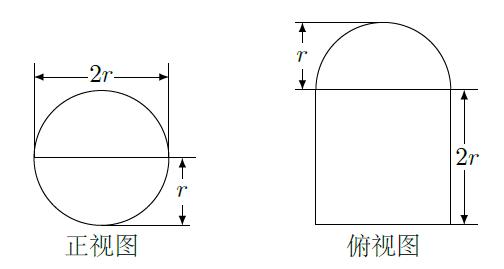
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
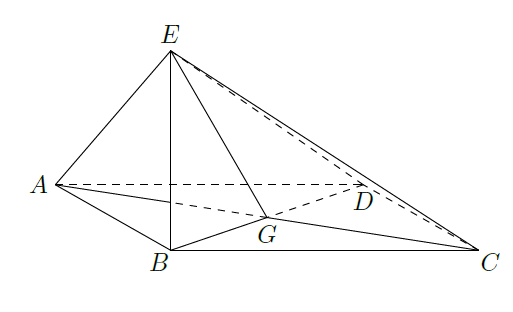
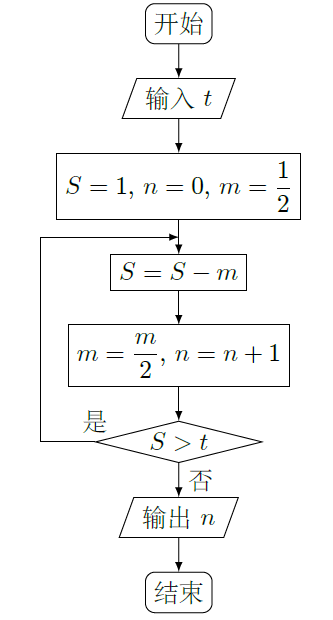
如图四边形
为菱形,
为
与
交点,
,
(Ⅰ)证明:平面
平面
;
(Ⅱ)若
,三棱锥
的体积为
,求该三棱锥的侧面积.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
(单位:千元)对年销售量
(单位:
)和年利润
(单位:千元)的影响,对近8年的宣传费
和年销售量
数据作了初步处理,得到下面的散点图及一些统计量的值.
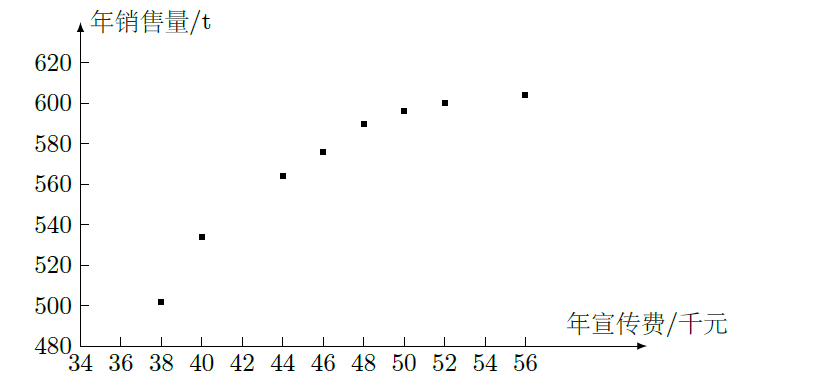

|
||||||
| 46.6 |
56.3 |
6.8 |
289.8 |
1.6 |
1469 |
108.8 |
表中 =  ,  =
(Ⅰ)根据散点图判断,
与
,哪一个适宜作为年销售量
关于年宣传费
的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(III)已知这种产品的年利润z与x,y的关系为
 ,根据(Ⅱ)的结果回答下列问题:
(Ⅰ)当年宣传费
时,年销售量及年利润的预报值时多少?
(Ⅱ)当年宣传费
为何值时,年利润的预报值最大?
附:对于一组数据
,
,……,
,其回归线
的斜率和截距的最小二乘估计分别为:
,
已知过点
且斜率为
的直线
与圆
交于
两点.
(Ⅰ)求
的取值范围;
(Ⅱ)
,其中
为坐标原点,求
.
如图
是圆
直径,
是
切线,
交
与点
.
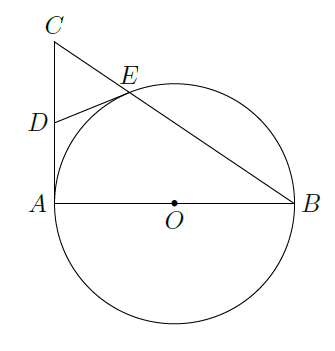
(Ⅰ)若
为
中点,求证:
是
切线;
(Ⅱ)若
,求
的大小.
在直角坐标系中,直线,圆,以坐标原点为极点,轴正半轴为极轴建立极坐标系.
(Ⅰ)求的极坐标方程.
(Ⅱ)若直线的极坐标方程为,设的交点为,求的面积.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号