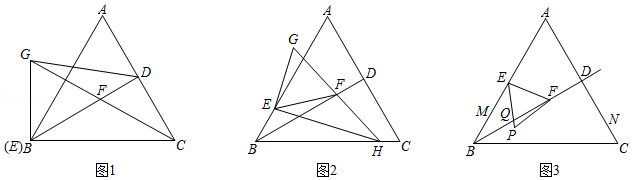
在等边 中, , ,垂足为 ,点 为 边上一点,点 为直线 上一点,连接 .
(1)将线段 绕点 逆时针旋转 得到线段 ,连接 .
①如图1,当点 与点 重合,且 的延长线过点 时,连接 ,求线段 的长;
②如图2,点 不与点 , 重合, 的延长线交 边于点 ,连接 ,求证: ;
(2)如图3,当点 为 中点时,点 为 中点,点 在边 上,且 ,点 从 中点 沿射线 运动,将线段 绕点 顺时针旋转 得到线段 ,连接 ,当 最小时,直接写出 的面积.
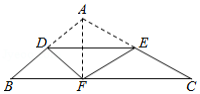
如图, 中,点 为边 的中点,连接 ,将 沿直线 翻折至 所在平面内,得 ,连接 ,分别与边 交于点 ,与 交于点 .若 , ,则 的长为 .

如图,在建筑物 左侧距楼底 点水平距离150米的 处有一山坡,斜坡 的坡度(或坡比)为 ,坡顶 到 的垂直距离 米(点 , , , , 在同一平面内),在点 处测得建筑物顶 点的仰角为 ,则建筑物 的高度约为
(参考数据: ; ;

| A. |
69.2米 |
B. |
73.1米 |
C. |
80.0米 |
D. |
85.7米 |
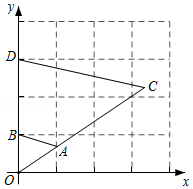
如图,在平面直角坐标系中,将 以原点 为位似中心放大后得到 ,若 , ,则 与 的相似比是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,三角形纸片 中,点 , , 分别在边 , , 上, , ,将这张纸片沿直线 翻折,点 与点 重合.若 , ,则四边形 的面积为 .
如图,相邻两个山坡上,分别有垂直于水平面的通信基站 和 .甲在山脚点 处测得通信基站顶端 的仰角为 ,测得点 距离通信基站 的水平距离 为 ;乙在另一座山脚点 处测得点 距离通信基站 的水平距离 为 ,测得山坡 的坡度 .若 ,点 , , , 在同一水平线上,则两个通信基站顶端 与顶端 的高度差为(参考数据: ,

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 与 位似,点 是它们的位似中心,其中 ,则 与 的周长之比是

| A. |
|
B. |
|
C. |
|
D. |
|
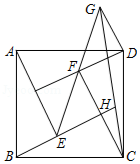
如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

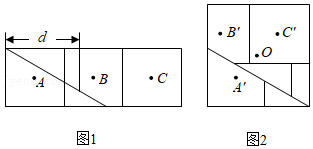
如图中 与 的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案,它由7个图形组成,请按以下要求选择其中一个并在图2、图3中画出相应的格点图形(顶点均在格点上).
(1)选一个四边形画在图2中,使点 为它的一个顶点,并画出将它向右平移3个单位后所得的图形.
(2)选一个合适的三角形,将它的各边长扩大到原来的 倍,画在图3中.

图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图 ,则图1中所标注的 的值为 ;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为 .
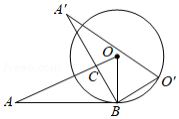
如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到△ ,使点 落在 上,边 交线段 于点 .若 ,则
度.
由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连结 ,延长 交 于点 .若 ,则 的值为
| A. |
|
B. |
|
C. |
|
D. |
|
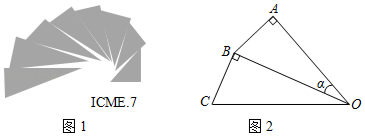
图1是第七届国际数学教育大会 会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 , ,则 的值为
| A. |
|
B. |
|
C. |
|
D. |
|
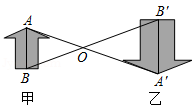
如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为
| A. |
8 |
B. |
9 |
C. |
10 |
D. |
15 |