命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立,命题q:指数函数f(x)=(3﹣2a)x是增函数,若p∨q为真,p∧q为假,求实数a的取值范围.
下面式子正确的是()
| A.5﹣0.2>5﹣0.1 |
| B.lge>lg3 |
| C.0.10.8<0.20.8 |
| D.log3π<log20.8 |
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M 成立,则称f(x)是D上的有界函数,其中M称为函f(x)的一个上界.已知函数f(x)=1+a +
+ ,g(x)=
,g(x)=
 .
.
(1)若函数g(x)为奇函数,求实数a的值;
(2)在(1)的条件下,求函数g(x),在区间[ ,3]上的所有上界构成的集合;
,3]上的所有上界构成的集合;
(3)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a•2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围.
已知函数f(x)=a|x+b|(a>0,a≠1,b∈R).
(1)若f(x)为偶函数,求b的值;
(2)若f(x)在区间[2,+∞)上是增函数,试求a、b应满足的条件.
设函数f(x)=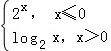 ,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是()
,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是()
| A.1 | B.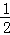 |
C. |
D.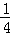 |
当x<0时,函数f(x)=(2a﹣1)x的值恒大于1,则实数a的取值范围是()
A.( ,1) ,1) |
B.(1,2) | C.(1,+∞) | D.(﹣∞,1) |
函数f(x)=ax﹣1+3的图象一定过定点P,则P点的坐标是 .
如果一个点既在对数函数的图象上又在指数函数的图象上,那么称这个点为“幸运点”,在下列的五个点M(1,1),N(1,2),P(2,1),Q(2,2),G(2, )中,“幸运点”有多少个()
)中,“幸运点”有多少个()
| A.0 | B.1 | C.2 | D.3 |