(1)计算:(2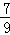 )
)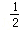 +(lg5)0+(
+(lg5)0+(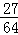 )
) ;
;
(2)解方程:log3(6x﹣9)=3.
已知f(x)=2x,g(x)是一次函数,并且点(2,2)在函数f[g(x)]的图象上,点(2,5)在函数g[f(x)]的图象上,求g(x)的解析式.
(1)函数f(x)=loga(2x﹣1)﹣1的图象过定点(1,0);
(2)已知函数f(x)是定义在R上的偶函数,当x≤0时,f(x)=x(x+1),则f(x)的解析式为f(x)=x2﹣|x|;
(3)若loga >1,则a的取值范围是(
>1,则a的取值范围是( ,1);
,1);
(4)若2﹣x﹣2y>lnx﹣ln(﹣y)(x>0,y<0),则x+y<0.
其中所有正确命题的序号是 .
(1)若xlog32=1,试求4x+4﹣x的值;
(2)计算:(2 )
) ﹣(﹣9.6)0﹣(3
﹣(﹣9.6)0﹣(3 )
) +(1.5)﹣2+(
+(1.5)﹣2+( ×
× )4.
)4.
设a=log0.50.9,b=log1.10.9,c=1.10.9,则a,b,c的大小关系为( )
| A.a<b<c | B.b<a<c | C.b<c<a | D.a<c<b |
函数g(x)=2015x+m图象不过第二象限,则m的取值范围是( )
| A.m≤﹣1 | B.m<﹣1 |
| C.m≤﹣2015 | D.m<﹣2015 |
已知函数f(x)=ax﹣1(a>0且a≠1)
(1)若函数y=f(x)的图象经过P(3,4)点,求a的值;
(2)比较 与f(﹣2.1)大小,并写出比较过程.
与f(﹣2.1)大小,并写出比较过程.