高中数学坐标系与参数方程试题

设 $a\in R$，直线 $\mathit{ax}-y+2=0$和圆 $\left\{\begin{array}{c}x=2+2\cos \theta ,\\ y=1+2\sin \theta \end{array}\right.$（ $\theta$为参数）相切，则 $a$的值为_____________．

在极坐标系中，已知两点 $A(3,\frac{\pi }{4}),B(\sqrt{2},\frac{\pi }{2})$ ，直线l的方程为 $\rho \sin (\theta +\frac{\pi }{4})=3$ .

（1）求 A， B两点间的距离；

（2）求点 B到直线 l的距离.

抛物线x²+4y=0的准线方程是 ．

双曲线x²﹣2y²=1的渐近线方程是（）

A．x±y=0

B．x±2y=0

C．

D．

过抛物线y²=4x的焦点作直线交抛物线于A（x₁，y₁），B（x₂，y₂）两点，若x₁+x₂=6，则|AB|= ．

已知F₁，F₂是双曲线=1（a，b＞0）的左、右焦点，过F₁且垂直于x轴的直线与双曲线交于A，B两点，若△ABF₂为钝角三角形，则该双曲线的离心率e的取值范围是（）

A．（1，+∞）

B．

C．

D．

抛物线x²=y的焦点坐标为（）

A．（，0）

B．（0，）

C．（，0）

D．（0，）

已知函数f（x）=x²+2x+1﹣2^x，则y=f（x）的图象大致为（）

A．

B．

C．

D．

已知双曲线﹣=1（a＞0，b＞0）的渐近线方程为y=±2x，则其离心率为（）

A．5

B．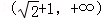

C．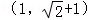

D．

在平面直角坐标系xOy中，抛物线x²=2py（p＞0）上纵坐标为1的点到焦点的距离为3，则焦点到准线的距离为（）

A．2

B．8

C．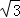

D．4

选修；坐标系与参数方程
在直角坐标系中，直线的参数方程为（为参数），若以原点为极点，轴正半轴为极轴建立极坐标系，已知圆的极坐标方程为，设是圆上任一点，连结并延长到，使．
（Ⅰ）求点轨迹的直角坐标方程；
（Ⅱ）若直线与点轨迹相交于两点，点的直角坐标为，求的值．

选修：坐标系与参数方程
在平面直角坐标系中，直线经过点，其倾斜角是，以原点为极点，以轴的非负半轴为极轴，与直角坐标系取相同的长度单位，建立极坐标系．设曲线的极坐标方程是．
（Ⅰ）若直线和曲线有公共点，求倾斜角的取值范围；
（Ⅱ）设为曲线任意一点，求的取值范围．

选修：坐标系与参数方程
在平面直角坐标系中，直线经过点，其倾斜角是，以原点为极点，以轴的非负半轴为极轴，与直角坐标系取相同的长度单位，建立极坐标系．设曲线的极坐标方程是．
（Ⅰ）若直线和曲线有公共点，求倾斜角的取值范围；
（Ⅱ）设为曲线任意一点，求的取值范围．

选修4-4:坐标系与参数方程
在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线和曲线（为参数）．
（1）将与的方程化为普通方程；
（2）判定直线l与曲线 是否相交，若相交求出被截得的弦长．

已知双曲线的一条渐近线过点（2，），则双曲线的离心率为（）

A．

B．

C．

D．