初中数学填空题

如图，正方形ABCD的边长为2，将长为2的线段QF的两端放在正方形相邻的两边上同时滑动．如果点Q从点A出发，沿图中所示方向按A→B→C→D→A滑动到点A为止，同时点F从点B出发，沿图中所示方向按B→C→D→A→B滑动到点B为止，那么在这个过程中，线段QF的中点M所经过的路线围成的图形的面积为      ．

如图，点A为⊙O上一个动点，点B在⊙O内，且OA=2，OB=2，当∠OAB的度数取最大值时，AB的长度为   ．

如图，已知∠AOB在平面直角坐标系的第一象限中，且∠AOB=30°，其两边分别交反比例函数y=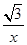在第一象限内的图象于A、B两点，连结AB，当∠AOB绕点O转动时，线段AB的最小值为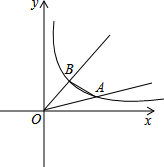       

读取表格中的信息，解决问题.满足＞1000的n可以取得的最小正整数是      .

n=1
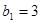n=2
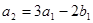n=3
…	…	…

 

如图，平面直角坐标系中，A（-3，0），B（0，4），对△AOB按图示的方式连续作旋转变换，这样得到的第2014个三角形中，A点的对应点的坐标为           .

如图，AB为⊙O的直径，AB=30，正方形DEFG的四个顶点分别在半径OA、OC及⊙O上，且∠AOC=45°，则正方形DEFG的面积为         ．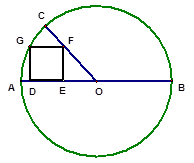

将一些半径相同的小圆按如图所示的规律摆放，请仔细观察，第 n 个图形有        个小圆．（用含 n 的代数式表示）

【改编题】如图，OP＝1，过P作PP₁⊥OP且PP₁＝1，得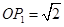；再过P₁作P₁P₂⊥OP₁且P₁P₂＝1，得；又过P₂作P₂P₃⊥OP₂且P₂P₃＝1，得OP₃＝2……依此法继续作下去，得＝________．

【改编】如图，直线AB，CD相交于点O，OE⊥AB，∠BOD：∠AOE=1：3，则∠AOD等于        度．

如图，在等腰Rt△OAA₁中，∠OAA₁=90°，OA=1，以OA₁为直角边作等腰Rt△OA₁A₂，以OA₂为直角边作等腰Rt△OA₂A₃，…则OA₄的长度为        ．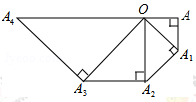

如图，在⊿ABC中，∠A﹤90°，∠C=30°，AB=4，BC=6，E为AB的中点，P为AC边上一动点，将⊿ABC绕点B逆时针旋转角（）得到，点P的对应点为，连，在旋转过程中，线段的长度的最小值是        ．

如图，AB是⊙O的直径，弦BC=4㎝，F是弦BC的中点，∠ABC=60°，若动点E以1 ㎝/s的速度从A点出发在AB上沿着A→B→A运动，设运动时间为t（s）（0≤t＜16），连接EF，当△BEF是直角三角形时，t（s）的值为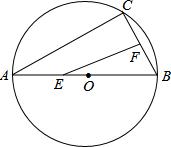                 

如图，在直角坐标系中，四边形ABCD是正方形，A（1，-1）、B（-1，-1）、C（-1，1）、D（1， 1）.曲线AAAA…叫做“正方形的渐开线”，其中、、…的圆心依次是点B、C、D、A循环，则点A的坐标是          .

如图，A、B的坐标分别为(1，0)、(0，2)，若将线段AB平移到至A₁B₁，A₁、B₁的坐标分别为(2，a)、(b，3)，则a＋b＝________．

在平面直角坐标系xOy中，对于点P(x，y)我们把点P′(－y＋1，x＋1)叫做点P的伴随点，已知点A₁的伴随点为A₂，点A₂的伴随点为A₃，点A₃的伴随点为A₄，这样依次得到A₁，A₂，A₃，…，A_n，…，若点A₁的坐标为(3，1)，则点A₃的坐标为________，点A₂₀₁₄的坐标为________；若点A₁的坐标为(a，b)，对于任意的正整数n，点A_n均在x轴上方，则a，b应满足的条件为________．