如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC= CE,F、G分别是BC、CE的中点,FM∥AC,GE∥DC、设图中三个平行四边形的面积依次是
CE,F、G分别是BC、CE的中点,FM∥AC,GE∥DC、设图中三个平行四边形的面积依次是 、
、 、
、 ,若
,若 ,则
,则 = .
= .
如图,在平面直角坐标系中,O为坐标原点,⊙O的半径为5,点B的坐标为(3,0),点A为⊙O上一动点,当∠OAB取最大值时,点A的坐标为 . 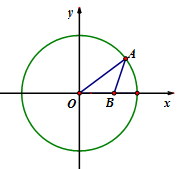
如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y= x上一点,则点B与其对应点B′间的距离为 .
x上一点,则点B与其对应点B′间的距离为 .
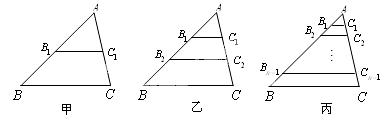
在△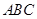 中,
中,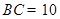 ,如图甲
,如图甲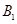 是
是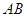 的中点,
的中点, ∥
∥ ,则
,则 = ,如图乙,
= ,如图乙,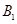 、
、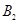 是
是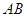 的三等分点,
的三等分点, ∥
∥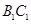 ∥
∥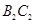 ,则
,则 +
+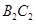 = ,如图丙,
= ,如图丙,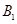 、
、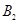 、…、
、…、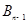 是
是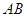 的
的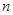 等分点,
等分点, ∥
∥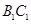 ∥
∥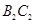 ∥…∥
∥…∥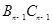 ,则
,则 +
+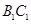 +
+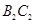 +…+
+…+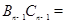 .
.
如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为 
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为______________.
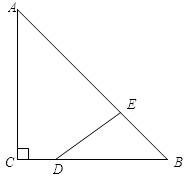
如图,Rt△ABC中,∠ACB=90°,AC=BC=4cm,CD=1cm,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,至A点结束,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为 秒。
如图,正方形ABCD的边长为4+2 ,点E在对角线BD上,且∠BAE=
,点E在对角线BD上,且∠BAE= ,EF⊥AB,垂足为点F,则EF的长是
,EF⊥AB,垂足为点F,则EF的长是 
在平面直角坐标系 O
O 中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒
中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D 点P从点O出发,以每秒 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形。
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒,当t为 时,△PQB为直角三角形。
如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=12,BD=16,E为AD中点,点P在x轴上移动.若△POE为等腰三角形,请写出所有符合要求的点P的坐标 .
如图,在平面直角坐标系中, 矩形AOBC的顶点A、B的坐标分别是A(0, 4) 、B( , 0) 作点A关于直线
, 0) 作点A关于直线 的对称点P,若△POB为等腰三角形, 则点P的坐标为 .
的对称点P,若△POB为等腰三角形, 则点P的坐标为 .
如图,在边长为10的菱形ABCD中,对角线BD ="16." 点E是AB的中点,P、Q是BD上的动点,且始终保持PQ ="2." 则四边形AEPQ周长的最小值为_________.(结果保留根号)