初中数学解答题

雨伞的中截面如图所示，伞骨AB＝AC，支撑杆OE＝OF，AE＝AB，AF＝AC，当O沿AD滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD与∠CAD有何关系？说明理由．

计算
（1）解不等式：5（x﹣2）﹣2（x+1）＞3．
（2）解不等式≤，并求出它的非负整数解。

已知△ABC，利用直尺和圆规，根据下列要求作图（保留作图痕迹，不要求写作法）．

（1）作∠ABC的平分线BD交AC于点D；
（2）作线段BD的垂直平分线交AB于点E，交BC于点F．

寻找公式，求代数式的值：从2开始，连续的偶数相加，它们的和的情况如下表：

（1）当n个最小的连续正偶数相加时，它们的和S与n之间的关系，用公式表示为_________________；
（2）并按此规律计算： ①2+4+6+…+300的值；  ②162+164+166+…+400的值．

如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形．

（1）你认为图②中的阴影部分的正方形的边长等于        ．
（2）请用两种不同的方法列代数式表示图②中阴影部分的面积，
方法①                    ．方法②                    ．
（3）观察图②，你能写出（m＋n）²，（m－n）²，mn这三个代数式之间的等量关系吗？
（4）根据（3）题中的等量关系，解决如下问题：若a＋b＝6，ab＝4，则求（a－b）²的值．

为庆祝我国首个空间实验室“天宫一号”顺利升空，学校开展了火箭模型制作比赛，如图为火箭模型的截面图，下面是梯形，中间是长方形，上面是三角形．

（1） 用a、b的代数式表示该截面的面积S；
（2） 当a＝2cm，b＝3cm时，求这个截面的面积．

解答
（1）化简及求值5（3a²b－2ab²）－4（－2 ab²＋3a²b） ，其中a、b满足|a＋2|＋（b－1）²＝0．
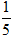（2）已知x＋y＝，xy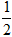＝－．求代数式（x＋3y－3xy）－2（xy－2 x－y） 的值．

解方程
（1） 2（3－x）＝－4x＋5         
（2）＝＋1

如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm．

（1）若P、Q是△ABC边上的两个动点，其中点P从A沿A→B方向运动，速度为每秒1cm，点Q从B沿B→C方向运动，速度为每秒2cm，两点同时出发，设出发时间为t秒．①当t=1秒时，求PQ的长；②从出发几秒钟后，△PQB是等腰三角形？
（2）若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动，则当点M在边CA上运动时，求△BCM成为等腰三角形时M运动的时间．

如图，△ACB和△ECD都是等腰直角三角形，A、C、D三点在同一直线上，连接BD、AE，并延长AE交BD于F．

（1）求证：△ACE≌△BCD；
（2）直线AE与BD互相垂直吗?请证明你的结论．

如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．

（1）求证：△ABQ≌△CAP；
（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．
（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．

已知点O到的两边AB、AC所在直线的距离相等，且OB＝OC．

（1）如图1，若点O在边BC上，求证：AB=AC；
（2）如图2，若点O在的内部，求证：AB=AC；
（3）若点O在的外部，AB=AC成立吗？请画图表示．

某市的A地和B地秋季育苗，急需化肥分别为90吨和60吨，该市的C地和D地分别储存化肥100吨和50吨，全部调配给A地和B地，已知从C、D两地运化肥到A、B两地的运费（元/吨）如下表所示

（1）设C地运到A地的化肥为吨，用含（吨）的代数式表示总运费W（元）
（2）求最低总运费，并说明总运费最低时的运送方案
（3）若总运费不少于5680元，共有几种方案？（化肥吨数取整数）

如图，BE⊥AC、CF⊥AB于点E、F，BE与CF交于点D，DE=DF，连接AD．

求证：（1）∠FAD=∠EAD；（2）BD=CD．                    

如图，正方形网格中每一个小正方形的边长都为1，每一个小格的顶点叫做格点．以格点为顶点分别按下列要求画三角形：

（1）在图1中，画一个三角形，使它的边长都是有理数；
（2）在图2、图3中分别画一个直角三角形，使它们的边长都是无理数，并且要求两个三角形不全等．