初中数学解答题

某品牌电脑销售公司有营销员14人，销售部为制定营销人员月销售电脑定额，统计了这14人某月的销售量如下（单位：台）：

销售量	200	170	130	80	50	40
人 数	1	1	2	5	3	2

 
（1）求这14位营销员该月销售该品牌电脑的平均数、中位数和众数．
（2）销售部经理把每位营销员月销售量定为90台，你认为是否合理？为什么?

（1）已知二次函数的图像经过点（-2，8）和（-1，5），求这个函数的表达式；
（2）已知抛物线的顶点为（－1，－3），与轴交点为（0，－5），求抛物线的解析式．

从2开始，连续的偶数相加，它们和的情况如下表：

加数的个数n	S
1	2=1×2
2	2＋4=6=2×3
3	2＋4＋6=12=3×4
4	2＋4＋6＋8=20=4×5
5	2＋4＋6＋8＋10=30=5×6

 
（1）若n=8时，则S的值为_____________．
（2）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=__________________．
（3）根据上题的规律计算2+4+6+8+10+…+98+100的值．

出租车司机小石某天下午营运全是在东西走向的人民大街上进行的，如果规定向东为正，向西为负，他这天下午行车里程（单位：千米）如下：
+15，-3，+14，-11，+10，-12．
（1）将最后一名乘客送达目的地时，小石距下午出发地点的距离是多少千米？
（2）若汽车耗油量为0．3升/千米，这天下午汽车耗油共多少升？

已知互为倒数，互为相反数，的绝对值为2，求的值

（1）若我们把不小于x的最小整数记作〈x〉，如〈2．4〉=3，〈－1．5〉=－1；则〈3〉=      ，〈－2．2〉=      
（2）在我国，出租车已经普及，杭州城区A、B两种出租车，它们的收费方式有所不同， A种出租车的收费方式是：每千米收费2．5元，不收其它费用。B种出租车的收费方式是：行程不超过3千米收费8元，超过3千米后超出部分每千米再增收2元，同时每趟营运在计价器显示的金额外再向乘客加收1元的燃料附加费．（注：两种出租车在路程上不足1千米按1千米计算，如6．1千米应算成7千米）若某公司员工小王需要乘出租车到离家x千米的公司上班。
①请利用题（1）中的符号，用代数式表示小王分别使用A、B两种出租车的收费情况。
②分别求出x=4．5；x=6；x=6．1时A、B两种出租车的收费情况．
③结合②的答案请说一说小王为了省钱应该如何选择出租车。

某餐厅中，一张桌子可坐6人，有以下两种摆放方式：
（1）当有张桌子时，两种摆放方式各能坐多少人？
（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？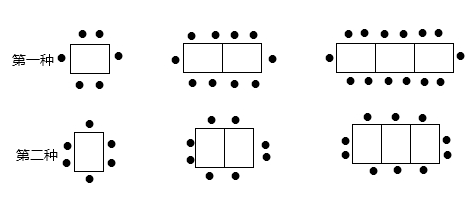

出租车司机小张某天上午营运全是在东西走向的政府大道上进行的，如果规定向东为正，向西为负，他这天上午的行程是（单位：千米）：＋15，－3，＋16，－11，＋10，－12，＋4，－15，＋16，－18．
（1）将最后一名乘客送达目的地时，小张距上午出发点的距离是多少千米？在出发点的什么方向？
（2）若汽车耗油量为0．6升/千米，出车时，邮箱有油72．2升，若小张将最后一名乘客送达目的地，再返回出发地，问小张今天上午是否需要加油？若要加油至少需要加多少才能返回出发地？若不用加油，请说明理由。

先化简，再求值
（1），其中。
（2）其中

某厂共有三个车间，一号车间有工人a人，二号车间人数比一号车间人数的２倍少一人，三号车间的人数比一号车间人数的一半多3个，全厂共有工人多少人？

将－2．5，，2，，，0在数轴上表示出来，并用“＜”把它们连接起来．

如图，AB⊥BC，射线CM⊥BC，且BC=5，AB=1，点P是线段BC （不与点B、C重合）上的动点，过点P作DP⊥AP交射线CM于点D，连结AD．

（1）如图1，若BP=4，求△ABP的周长．
（2）如图2，若DP平分∠ADC，试猜测PB和PC的数量关系，并说明理由．
（3）若△PDC是等腰三角形，作点B关于AP的对称点B′，连结B′D，则B′D=      ．（请直接写出答案）

如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．

（1）求证：△ABQ≌△CAP；
（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．
（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．

已知购买1个足球和1个篮球共需130元，购买2个足球和1个篮球共需180元．
（1）求每个足球和每个篮球的售价；
（2）如果某校计划购买这两种球共54个，总费用不超过4000元，问最多可买多少个篮球？

如图，某中学有一块四边形的空地ABCD，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，若每平方米草皮需要200元，问学校需要投入多少资金买草皮？