初中数学解答题

（1）2x²-9x+8=0（用公式法）         
（2）3x²-4x-6=0（配方法解）
（3）（x-2）²=（2x+3）²（用合适的方法）  
（4）（5x-1）²-3（5x-1）=0（用合适的方法）

如图，二次函数y=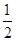x²+bx+c的图象交x轴于A、D两点，并经过B点，已知A点坐标是（2，0），B点的坐标是（8，6）．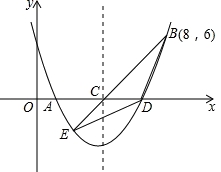

（1）求二次函数的解析式．
（2）求函数图象的顶点坐标及D点的坐标．
（3）该二次函数的对称轴交x轴于C点．连接BC，并延长BC交抛物线于E点，连接BD，DE，求△BDE的面积．
（4）抛物线上有一个动点P，与A，D两点构成△ADP，是否存在S_△ADP=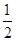S_△BCD？若存在，请求出P点的坐标；若不存在．请说明理由．

某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．
（1）现该商场要保证每天盈利6 000元，同时又要顾客得到实惠，那么每千克应涨价多少元？
（2）若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？

如图所示，在抛物线y=-x²上有A，B两点，其横坐标分别为1，2；在y轴上有一动点C，使AC+BC距离最短，求C点的坐标．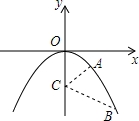

有一种传染性疾病，蔓延速度极快．据统汁，在人群密集的某城市里，通常情况下，每人一天能传染给若干人，通过计算解答下面的问题：
（1）现有一人患了这种疾病，开始两天共有225人患上此病，求每天一人传染了几人？
（2）两天后，人们有所觉察，这样平均一个人一天以少传播5人的速度在递减，求再过两天共有多少人患有此病？

已知：二次函数y=x²+bx-3的图象经过点A（2，5）．
（1）求二次函数的解析式；
（2）求二次函数的图象与x轴的交点坐标；
（3）将（1）中求得的函数解析式用配方法化成y=（x-h）²+k的形式．

解方程
（1）（x-1）²=4
（2）3x²+5（2x+1）=0
（3）x²-3x-4=0
（4）（y+2）²=（3y-1）²．

已知二次函数的图像经过点P（0，）、A（5，0）、B（1，0）．

（1）求该二次函数的解析式；
（2）点C在该二次函数的图像上，当△ABC的面积为12时，求点C坐标；
（3）在（2）的条件下，求△ABC外接圆圆心点D的坐标．

已知二次函数中，函数与自变量的部分对应值如下表：

	…	-1	0	1	2	3	4	…
	…	-8	-3	0	1	0	-3	…

 
（1）求该二次函数的关系式；
（2）当为何值时，有最大值，最大值是多少？
（3）若，两点都在该函数的图象上，试比较与的大小．

如图，在Rt△ABC中，∠B=90°，AB=" 3" cm，BC=" 4" cm．点P从点A出发，以1 cm／s的速度沿AB运动；同时，点Q从点B出发，以2 cm／s的速度沿BC运动．当点Q到达点C时，P、Q两点同时停止运动．

（1）试写出△PBQ的面积 S （cm²）与动点运动时间 t （s）之间的函数表达式；
（2）运动时间 t 为何值时，△PBQ的面积最大？最大值是多少？．

去年鱼塘里饲养鱼苗 10 千尾，平均每千尾的产量为 1000 kg．今年计划继续向鱼塘里投放鱼苗，预计每多投放鱼苗 1 千尾，每千尾鱼的产量将减少 50 kg，今年应投放鱼苗多少千尾，才能使总产量最大？最大总产量是多少？

某校九年级数学课外兴趣小组的同学积极参加义工活动，小庆对全体小组成员参加活动次数的情况进行统计分析，绘制了如下不完整的统计表和统计图（图）．

次数	10	8	6	5
人数	3	a	2	1

 
（1）表中a=    ；
（2）请将条形统计图补充完整；

（3）从小组成员中任选一人向学校汇报义工活动情况，参加了10次活动的成员被选中的概率有多少？

某篮球运动员去年共参加40场比赛，其中3分球的命中率为0．25，平均每场有6次3分球未投中．
（1）该运动员去年的比赛中共投中多少个3分球？
（2）在其中的一场比赛中，该运动员3分球共出手16次，小明说，该运动员这场比赛中一定投中了4个3分球，你认为小明的说法正确吗？请说明理由．

在一个暗箱中装有红、黄、白三种颜色的乒乓球（除颜色外其余均相同）．其中白球、黄球各1个，若从中任意摸出一个球是白球的概率是．
（1）求暗箱中红球的个数．
（2）先从暗箱中任意摸出一个球记下颜色后放回，再从暗箱中任意摸出一个球，求两次摸到的球颜色不同的概率（用树形图或列表法求解）．

在某公路标识牌路口，汽车可直行、可左转、可右转，若这三种可能性相同．
（1）用画树形图的方法，列出两辆汽车经过该路口的所有可能；
（2）求两辆汽车经过该路口都直行的概率．