如图,点A坐标为(-1,1),将此小船向左平移2个单位后,画出图形,并指出A,B,C,D各点坐标.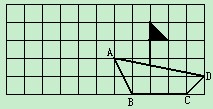
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD
向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于E
①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?
请直接写出相应的t值.
一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程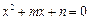 有两个不相等实数根的概率.
有两个不相等实数根的概率.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
如图9,边长为5的正方形 的顶点
的顶点 在坐标原点处,点
在坐标原点处,点 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点 是
是 边上的点(不与点
边上的点(不与点 重合),
重合), ,且与正方形外角平分线
,且与正方形外角平分线 交于点
交于点 .
.
(1)当点 坐标为
坐标为 时,试证明
时,试证明 ;
;
(2)如果将上述条件“点 坐标为(3,0)”改为“点
坐标为(3,0)”改为“点 坐标为(
坐标为( ,0)(
,0)( )”,结论
)”,结论 是否仍然成立,请说明理由;
是否仍然成立,请说明理由;
(3)在 轴上是否存在点
轴上是否存在点 ,使得四边形
,使得四边形 是平行四边形?若存在,用
是平行四边形?若存在,用 表示点
表示点
的坐标;若不存在,说明理由.
已知二次函数 的图象经过
的图象经过 和
和 三点
三点
(1)若该函数图象顶点恰为点 ,写出此时
,写出此时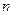 的值及
的值及 的最大值;
的最大值;
(2)当 时,确定这个二次函数的解析式,并判断此时
时,确定这个二次函数的解析式,并判断此时 是否有最大值;
是否有最大值;
(3)由(1)、(2)可知,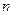 的取值变化,会影响该函数图象的开口方向.请你求出
的取值变化,会影响该函数图象的开口方向.请你求出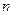 满足
满足
什么条件时, 有最小值?
有最小值?
2010年6月4日,乌鲁木齐市政府通报了首府2009年环境质量公报,其中空气质量级别分布统计图如图8所示,请根据统计图解答以下问题:
(1)写出2009年乌鲁木齐市全年三级轻度污染天数:
(2)求出空气质量为二级所对应扇形圆心角的度数(结果保留到个位);
(3)若到2012年,首府空气质量良好(二级及二级以上)的天数与全年天数(2012年是闰年,全年有366天)之比超过85%,求2012年空气质量良好的天数要比2009年至少增加多少天?
2010年5月中央召开了新疆工作座谈会,为实现新疆跨越式发展和长治久安,作出了重要战略决策部署.为此我市抓住机遇,加快发展,决定今年投入5亿元用于城市基础设施维护和建设,以后逐年增加,计划到2012年当年用于城市基础设施维护与建设资金达到8.45亿元.
(1)求从2010年至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率;
(2)若2010年至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率相同,
预计我市这三年用于城市基础设施维护和建设资金共多少亿元?
某过街天桥的截面图为梯形,如图7所示,其中天桥斜面 的坡度为
的坡度为
( 是指铅直高度
是指铅直高度 与水平宽度
与水平宽度 的比),
的比), 的长为10m,天桥另一斜面
的长为10m,天桥另一斜面
坡角 =
= .
.
(1)写出过街天桥斜面 的坡度;
的坡度;
(2)求 的长;
的长;
(3)若决定对该过街天桥进行改建,使 斜面的坡度变缓,将其
斜面的坡度变缓,将其 坡角改为
坡角改为 ,
,
方便群众,改建后斜面为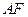 .试计算此改建需占路面的宽度
.试计算此改建需占路面的宽度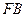 的长(结果精确0.01)
的长(结果精确0.01)
如图6,在平面直角坐标系中,直线 分别交
分别交 轴、
轴、 轴于点
轴于点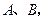 将
将 绕点
绕点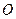 顺时针旋转90
顺时针旋转90 后得到
后得到 .
.
(1)求直线 的解析式;
的解析式;
(2)若直线 与直线
与直线 相交于点
相交于点 ,求
,求 的面积.
的面积.
如图5,在平行四边形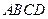 中,
中,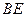 平分
平分 交
交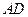 于点
于点 ,
, 平分
平分
 交
交 于点
于点 .
.
求证:(1) ;
;
(2)若 ,则判断四边形
,则判断四边形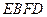 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论.