如图,直线y=kx+2与x轴、y轴分别交于点A、
B,点C(1,a)是直线与双曲线 的一个交点,过点C作
的一个交点,过点C作
CD⊥y轴,垂足为D,且△BCD的面积为1.
(1)求双曲线的解析式 与直线AB的解析式:
与直线AB的解析式:
(2)若在y轴上有一点E,使得以E、A、B为顶点的三角形与
△BCD相似,求点E的坐标.
现有一张宽为12cm练习纸,相邻两条格线间的距离均为0.8cm.调皮的小聪在
纸的左上角用印章印出一个矩形卡通图案,图案的顶点恰好在四条格线上,测得∠a=32°.
(1)求矩形图案的面积:
(2)若小聪在第一个图案的右边以同样的方式继续盖印(如图),最多一共能印几个完整的图
案?(参考数据:sin32 °≈0.5,cos32°≈0.8,tan32°≈0.6)
°≈0.5,cos32°≈0.8,tan32°≈0.6)
如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1 秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;
秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?
某体育彩票经销商计划用45000元从省体彩中心购进彩票20扎,每扎1 0 00张,
00张,
已知体彩中心有A、B、C三种不同价格的彩票,进价分别是A彩票每张1.5元, B彩票每
B彩票每
张2元,C彩票每张2.5元.
(1)若经销商同时购进两种不同型号的彩票20扎,并将45000元恰好用完,请你帮助经销商
设计进票方案:
(2)若销售A型彩票一张获手续费0.2元,B型彩票一张获手续费0.3元,C型彩票一张获手续费0.5元.在问题(1)设计的购进两种彩票的方案中,为使销售完时获得的手续费最多,你选择哪种进票方案?
(3)若经销商准备用45 000元同时购进A、B、C三种彩票20扎,请你帮助经销商设计一种
进票方案.(直接写出答案)
如图,已知∠AOB=120°,OM平分∠AOB,将正三角形的一个顶点P放在射
线OM上,两边分别与OA、OB交于点C、D.
(1)如图①若边PC和OA垂直,那么线段PC和PD相等吗?为什么?
(2)如图②将正三角形绕P点转过一角度,设两边与OA、OB分别交于C',D',那么线段PC'
和PD'相等吗?为什么?
某初级中学为了解学生的身高状况,在1500名学生中抽取部分学生进行抽样统计,结果如下:
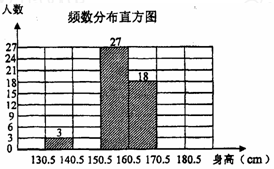
请你根据上面的图表,解答下列问题:
(1)此次抽样调查中样本容量为 ;
(2)m= ,n= ;
(3)补全频数分布直方图;
(4)请你估计该校1500名学生中身高处于160.5~170.5cm的人数约为 人.
如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B. (1)求证:△ABC≌△CDE;
(1)求证:△ABC≌△CDE;
(2)若∠A=40°求∠BCD的度数.
如图(十一)所示,在平面直角坐标系Oxy中,已知点A(-,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C.
(1)求∠ACB的度数;
(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形.若存在,则求出所有 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.
数学课堂上,徐老师出示一道试题:
如图(十)所示,在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
(1)经过思考,小明展示了一种正确的证明过程.请你将证明过程补充完整.
证明:在AB上截取EA=MC,连结EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,∴∠1=∠2.
又CN平分∠ACP,∠4=∠ACP=60°.∴∠MCN=∠3+∠4=120°…………①
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM.
∴△BEM为等边三角形.∴∠6=60°.
∴∠5=180°-∠6=120°.………②
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵
∴△AEM≌△MCN (ASA).∴AM=MN.
(2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1.是否还成立?(直接写出答案,不需要证明)
(3) 若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠AnMnNn= °时,结论AnMn=MnNn仍然成立?(直接写出答案,不需要证明)

为庆祝建党90周年,某学校欲按如下规则组建一个学生合唱团参加我市的唱红歌比赛.
规则一:合唱队的总人数不得少于50人,且不得超过55人.
规则二:合唱队的队员中,九年级学生占合唱团宗人数的,八年级学生占合唱团总人数的,余下的为七年级学生.请求出该合唱团中七年级学生的人数.
某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了统计表及如图(九)所示的统计图.
| 零花钱数额(元) |
5 |
10 |
15 |
20 |
| 学生人数(个) |
a |
15 |
20 |
5 |
请根据图表中的信息回答以下问题.
(1)求a的值;
(2)求这50名学生每人一周内的零花钱数额的众数和平均数.