《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2卷“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.
(1)我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)

公式①:
公式②:
公式③:
公式④:
图1对应公式_____,图2对应公式_____,图3对应公式_____,图4对应公式_____.
(2)《几何原本》中记载了一种利用几何图形证明平方差公式 的方法,如图5,请写出证明过程;(已知图中各四边形均为矩形)
(3)如图6,在等腰直角三角形 中, , 为 的中点, 为边 上任意一点(不与端点重合),过点 作 于点 ,作 于点 ,过点 作 交 的延长线于点 .记 与 的面积之和为 , 与 的面积之和为 .
①若 为边 的中点,则 的值为_____;
②若 不为边 的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.

2022年的冬奥会在北京举行,其中冬奥会吉祥物“冰墩墩”深受人们喜爱,多地出现了“一墩难求”的场面.某纪念品商店在开始售卖当天提供 个“冰墩墩”后很快就被抢购一空,该店决定让当天未购买到的顾客可通过预约在第二天优先购买,并且从第二天起,每天比前一天多供应m个(m为正整数).经过连续15天的销售统计,得到第 天( ,且 为正整数)的供应量 (单位:个)和需求量 (单位:个)的部分数据如下表,其中需求量 与 满足某二次函数关系.(假设当天预约的顾客第二天都会购买,当天的需求量不包括前一天的预约数)
|
第 天 |
|
|
… |
|
… |
|
… |
|
|
供应量 (个) |
|
|
… |
|
… |
|
… |
|
|
需求量 (个) |
|
|
… |
|
… |
|
… |
|
(1)直接写出 与 和 与 的函数关系式;(不要求写出 的取值范围)
(2)已知从第 天开始,有需求的顾客都不需要预约就能购买到(即前 天的总需求量超过总供应量,前 天的总需求量不超过总供应量),求 的值;(参考数据:前 天的总需求量为 个)
(3)在第(2)问 取最小值的条件下,若每个“冰墩墩”售价为 元,求第 天与第 天的销售额.
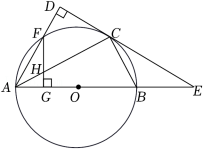
如图,已知 为 上一点,点 在直径 的延长线上, 与 相切,交 的延长线于点 ,且 .
(1)判断 与 的位置关系,并说明理由;
(2)若 , ,
①求 的半径;
②求 的长.

为落实国家“双减”政策,立德中学在课后托管时间里开展了“音乐社团、体育社团、文学社团、美术社团”活动.该校从全校 名学生中随机抽取了部分学生进行“你最喜欢哪一种社团活动(每人必选且只选一种)”的问卷调查,根据调查结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
(1)参加问卷调查的学生共有____人;
(2)条形统计图中m的值为____,扇形统计图中 的度数为____;
(3)根据调查结果,可估计该校 名学生中最喜欢“音乐社团”的约有____人;
(4)现从“文学社团”里表现优秀的甲、乙、丙、丁四名同学中随机选取两名参加演讲比赛,请用列表或画树状图的方法求出恰好选中甲和乙两名同学的概率.

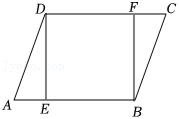
如图,在平行四边形 中,点 分别在边 上,且四边形 为正方形.
(1)求证: ;
(2)已知平行四边形 的面积为 , ,求 的长.
已知关于 的一元二次方程 有两个不等实数根 .
(1)求 的取值范围;
(2)若 ,求 的值.
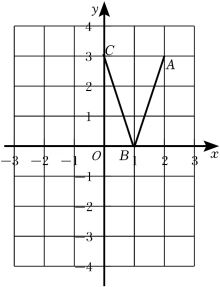
如图, 是 的直径,点 是圆上的一点, 于点 , 交 于点 ,连接 ,若 平分 ,过点 作 于点 交 于点 .
(1)求证: 是 的切线;
(2)延长 和 交于点 ,若 ,求 的值;
(3)在(2)的条件下,求 的值.
今年,某市举办了一届主题为“强国复兴有我”的中小学课本剧比赛.某队伍为参赛需租用一批服装,经了解,在甲商店租用服装比在乙商店租用服装每套多 元,用 元在甲商店租用服装的数量与用 元在乙商店租用服装的数量相等.
(1)求在甲,乙两个商店租用的服装每套各多少元?
(2)若租用 套以上服装,甲商店给以每套九折优惠.该参赛队伍准备租用 套服装,请问在哪家商店租用服装的费用较少,并说明理由.
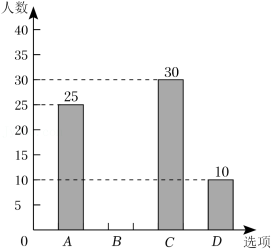
某校将举办的“壮乡三月三”民族运动会中共有四个项目:A跳长绳,B抛绣球,C拔河,D跳竹竿舞.该校学生会围绕“你最喜欢的项目是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
|
项目 |
内容 |
百分比 |
|
A |
跳长绳 |
|
|
B |
抛绣球 |
|
|
C |
拔河 |
|
|
D |
跳竹竿舞 |
|
请结合统计图表,回答下列问题:
(1)填空: _____;
(2)本次调查的学生总人数是多少?
(3)请将条形统计图补充完整;
(4)李红同学准备从抛绣球和跳竹竿舞两个项目中选择一项参加,但她拿不定主意,请你结合调查统计结果给她一些合理化建议进行选择.
如图,在平面直角坐标系中,形如英文字母“ ”的图形三个端点的坐标分别是 .
(1)画出“ ”字图形向左平移 个单位后的图形;
(2)画出原“ ”字图形关于x轴对称的图形;
(3)所得图形与原图形结合起来,你能从中看出什么英文字母?(任意答一个即可)