初中数学解答题

如图，有牌面数字都是2，3，4的两组牌．从毎组牌中各随机摸出一张，请用画树状图或列表的方法，求摸出的两张牌的牌面数字之和为6的概率．

将直线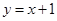向左平移2个单位后得到直线l，若直线l与反比例函数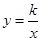的图象的交点为（2，-m）．
求直线l的解析式及直线l与两坐标轴的交点；
求反比例函数的解析式．

在2008年春运期间，我国南方出现大范围冰雪灾害，导致某地电路断电，该地供电局组织电工进行抢修。供电局距离抢修工地15千米，抢修车装载着所需材料先从供电局出发，15分钟后，电工乘吉普车从同一地点出发，结果他们同时到达抢修工地。已知吉普车速度是抢修车速度的1.5倍，求这两种车的速度.

已知：如图，在直角梯形中，，，，．
求直角梯形的面积；
点E是边上一点，过点作EF⊥DC于点F.求证．

已知：如图，AB⊥BE于点B，DE⊥BE于点E，F、C在BE上，AC、DF相交于点G，且AB＝DE，BF＝CE．
求证： GF＝GC．

以直线为对称轴的抛物线过点（3，0）,(0，3)，求此抛物线的解析式.

解方程： 

解方程：

解方程：      

某班甲、乙、丙三位同学进行了一次用正方形纸片折叠探究相关数学问题的课题学习活动.
活动情境：
如图2，将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G)，使点B落在AD边上的点 F处，FN与DC交于点M处，连接BF与EG交于点P．
所得结论：
当点F与AD的中点重合时：（如图1）甲、乙、丙三位同学各得到如下一个正确结论（或结果）：
甲：△AEF的边AE=     cm，EF=    cm；
乙：△FDM的周长为16 cm；
丙：EG=BF.
你的任务：
填充甲同学所得结果中的数据；
 写出在乙同学所得结果的求解过程；
当点F在AD边上除点A、D外的任何一处（如图2）时：
① 试问乙同学的结果是否发生变化？请证明你的结论；
② 丙同学的结论还成立吗？若不成立，请说明理由，若你认为成立，先证明EG=BF，再求出S（S为四边形AEGD的面积）与x（AF=x）的函数关系式，并问当x为何值时，S最大？最大值是多少？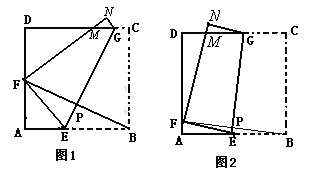

某校为了解初中生的交通安全知识掌握情况，在本校初中部随机抽取10﹪的学生，进行了交通安全知识测试，得分情况如下两个统计图，并约定85分及以上为优秀；73分～84分为良好；60分～72分为合格；59分及以下为不合格（满分为100分）．
在抽取的学生中,不合格人数所占的百分比是      ；
若不合格学生的总分恰好等于其他等级的某一个学生的分数，请推测这个学生是什么等级？并估算出该校初中部学生中共有多少人不合格？
试求所抽取的学生的平均分.
．

在2012年元旦期间有甲、乙两个小型超市举行有奖促销活动，顾客每购货20元就有一回按下面规则转盘获奖机会，且两超市奖额等同.规则是甲、乙两超市各把一转盘分成4个、3个区域，并标上了数字（如图甲、乙），顾客一回转盘要转两次，第一次与第二次分别停止后指针所指数字之和为奇数时就获奖（若指针停在等分线上，那么重转一次，直到指针指向某一份为止）.
利用树形图或列表法分别求出甲、乙两超市顾客一回转盘获奖的概率；
如果只考虑中奖因素，你将会选择去哪个超市购物？请说明理由．

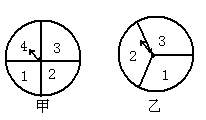
如图1，是某单位的透空护栏，如图2是它的示意图，它是用外径为3cm的圆钢管与外圆直径为15cm的圆圈焊接而成的（圆圈由扁钢筋做成，两圆钢管之间夹一个圆圈），若要做高度统一为2m，长为7.41m的护栏.试问：需要圆钢管和展直扁钢筋的总长度各是多少m？

在Rt△ABC中，∠ACB=90°，AB=4，D为AB的中点，将一直角△DEF纸片平放在△ACB所在的平面上，且使直角顶点重合于点D（C始终在△DEF内部），设纸片的两直角边分别与AC、BC相交于M、N.
当∠A=∠NDB=45°时，四边形MDNC的面积为       ；
当∠A=45°，∠NDB≠45°时，四边形MDNC的面积是否与（1）相同？说明理由；
当∠A=∠NDB=30°时，四边形MDNC的面积为       ；
当∠A=30°，∠NDB≠30°时，四边形MDNC的面积是否发生变化？若不发生变化（即与（3）相同），说明理由，若发生变化，设四边形MDNC的面积为S，BN为，求S与之间的关系.

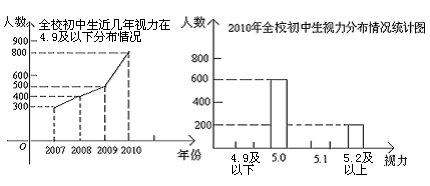
为了调查某校全体初中生的视力变化情况，统计了每位初中生连续三年视力检查的结果(如图1)，并统计了2010年全校初中生的视力分布情况（如图2、3）.

图2

图1

  从图1提供的信息用统计知识,预测2012年全校学生的视力在4.9及以下的学生人数（从一个角度预测即可）;

根据3幅图中提供的信息补全图2与图3；
学校计划在2012年加强用眼健康方面的教育.并通过治疗, 要求2010年视力在4.9及以下的部分假性近视的学生,视力达到5.0及以上.使2012年学校视力的达标率(视力在5.0及以上就算达标)上升10％,求这个学校在2012年视力好转、达标的假性近视学生的人数.