(本小题9分)如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)作出格点
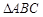 关于直线DE对称的
关于直线DE对称的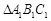 ;
;(2)作出
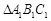 绕点
绕点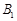 顺时针方向旋转90°后
顺时针方向旋转90°后 的
的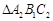 ;
;(3)求
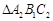 的周长.
的周长.
(本题6分)如图,平面内有A、B、C、D 四点,按下列语句画图: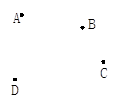
(1)画射线AB,直线BC,线段AC;
(2)延长CA;
(3)连接AD与BC相交于点E.
抛物线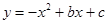 过点(0,-3)和(2,1),试确定抛物线的解析式,并求出抛物线与x轴的交点坐标.
过点(0,-3)和(2,1),试确定抛物线的解析式,并求出抛物线与x轴的交点坐标.
已知:如图,□ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.
求证:AB=AF.
某市为了解市民对已闭幕的某一博览会的总体印象,利用最新引进的“计算机辅助电话访问系统”(简称CATI系统),采取电脑随机抽样的方式,对本市年龄在16~65岁之间的居民,进行了400个电话抽样调查.并根据每个年龄段的抽查人数和该年龄段对博览会总体印象感到满意的人数绘制了下面的图(1)和图(2)(部分)
根据上图提供的信息回答下列问题:被抽查的居民中,人数最多的年龄段是 岁;
已知被抽查的400人中有83%的人对博览会总体印象感到满意,请你求出31~40岁年龄段的满意人数,并补全图(2);
比较31~40岁和41~50岁这两个年龄段对博览会总体印象满意率的高低(四舍五入到1%).注:某年龄段的满意率=该年龄段满意人数
 该年龄段被抽查人数
该年龄段被抽查人数 100%.
100%.

如图:把一张给定大小的矩形卡片ABCD放在宽度为10mm的横格纸中,恰好四个顶点都在横格线上,已知α=25°,求长方形卡片的周长。(精确到1mm,参考数据: sin25°≈0,cos25°≈0.9,tan25°≈0.5).
解应用题:
某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
| 类型 价格 |
A型 |
B型 |
| 进价(元/盏) |
40 |
65 |
| 标价(元/盏) |
60 |
100 |
这两种台灯各购进多少盏?
在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
初中生对待学习的态度一直是教育工作者关注的问题之一.为此,某区教委对该区部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).
请根据图中提供的信息,解答下列问题:此次抽样调查中,共调查了 名学生;
将图①补充完整;
求出图②中C级所占的圆心角的度数;
根据抽样调查结果,请你估计该区近20000名初中生中大
约有多少名学生学习态度达标(达标包括A级和B级)?
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分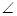 CAM交⊙O于D,过D作DE⊥MN于E.
CAM交⊙O于D,过D作DE⊥MN于E.求证:DE是⊙O的切线;
若
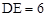 cm,
cm,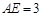 cm,求⊙O的半径.
cm,求⊙O的半径.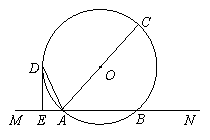
已知:如图,点E、F分别为□ABCD 的BC、AD边上的点,且∠1=∠2.
求证:AE=FC.