初中数学选择题

平面直角坐标系中，已知A（8，0），△AOP为等腰三角形且面积为16，满足条件的P点有（）

A．4个

B．8个

C．10个

D．12个

如图，点P是△ABC的边AC上一点，连接BP，以下条件中，不能判定△ABP∽△ACB的是（　　）

A．	B．
C．∠ABP＝∠C	D．∠APB＝∠ABC

如图，点A（3，n）在双曲线上，过点A作AC⊥x轴，垂足为C．线段OA的垂直平分线交OC于点B，则△ABC的周长是（　　）

A．8 B．6 C． D．4

在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB＝5，BC＝6，则CE＋CF的值为(　　)

A．

B．

C．或

D．或

已知A、B两地相距900m，甲、乙两人同时从A地出发，以相同速度匀速步行，20min后到达B地，甲随后马上沿原路按原速返回，回到A地后在原地等候乙回来；乙则在B地停留10min后也沿原路以原速返回A地，则甲、乙两人之间的距离s（m）与步行时间t（min）之间的函数关系可以用图象表示为（）
A． B．
C． D．

l00米长的小棒，第1次截去一半，第2次截去剩下的，第三次截去剩下的,如此下去，直到截去剩下的,则剩下的小棒长为（）米 。

A．20

B．15

C．1

D．50

如图，将正方形对折后展开（图④是连续两次对折后再展开），再按图示方法折叠，能够得到一个直角三角形（阴影部分），且它的一条直角边等于斜边的一半．这样的图形有

图①图②图③图④

A．4个

B．3个

C．2个

D．1个

有一批苹果需要装箱，若每箱装25千克，则有40千克装不下；若每箱装30千克，则除剩余20个空箱外其余箱子都装满，这批苹果共有（）

A．2760千克

B．3240千克

C．112千克

D．128千克

抛物线y=x²+mx+n可以由抛物线y=x²向上平移2个单位，再向左平移3个单位得到，则mn值为（）

A．6

B．12

C．54

D．66

如图，直线y=kx+c与抛物线y=ax²+bx+c的图象都经过y轴上的D点，抛物线与x轴交于A、B两点，其对称轴为直线x=1，且OA=OD．直线y=kx+c与x轴交于点C（点C在点B的右侧）．则下列命题中正确命题的个数是（）
①abc＞0；②3a+b＞0；③﹣1＜k＜0；④k＞a+b；⑤ac+k＞0．

A．1 B．2 C．3 D．4

如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y₁和过P、A两点的二次函数y₂的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=3时，这两个二次函数的最大值之和等于（）

A． B． C．3 D．4

这是一根起点为0的数轴，现有同学将它弯折，如图所示，例如：虚线上第一行0，第二行6，第三行21，…，第10行的数是（）

A．351

B．702

C．378

D．756

设 $O$ 为坐标原点，点 $A$ 、 $B$ 为抛物线 $y=x^2$ 上的两个动点，且 $\mathit{OA}\perp \mathit{OB}$ ．连接点 $A$ 、 $B$ ，过 $O$ 作 $\mathit{OC}\perp \mathit{AB}$ 于点 $C$ ，则点 $C$ 到 $y$ 轴距离的最大值 $($ 　　 $)$

A．

$\frac{1}{2}$

B．

$\frac{\sqrt{2}}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

1

如图，在△ABC中，AD平分∠BAC，按如下步骤作图：第一步，分别以点A、D为圆心，以大于AD的长为半径在AD两侧作弧，交于两点M、N；第二步，连接MN分别交AB、AC于点E、F；第三步，连接DE、DF．若BD=6，AF=4，CD=3，则BE的长是（）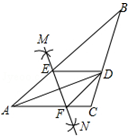

A．2 B．4 C．6 D．8

如图1，在矩形 $\mathit{ABCD}$中， $P$为 $\mathit{CD}$边上一点 $(\mathit{DP}<\mathit{CP})$， $\angle \mathit{APB}=90°$．将 $\mathit{\Delta ADP}$沿 $\mathit{AP}$翻折得到△ $\mathit{AD}\text{'}P$， $\mathit{PD}\text{'}$的延长线交边 $\mathit{AB}$于点 $M$，过点 $B$作 $\mathit{BN}//\mathit{MP}$交 $\mathit{DC}$于点 $N$．

（1）求证： $A{D}^2=\mathit{DP}·\mathit{PC}$；

（2）请判断四边形 $\mathit{PMBN}$的形状，并说明理由；

（3）如图2，连接 $\mathit{AC}$，分别交 $\mathit{PM}$， $\mathit{PB}$于点 $E$， $F$．若 $\frac{\mathit{DP}}{\mathit{AD}}=\frac{1}{2}$，求 $\frac{\mathit{EF}}{\mathit{AE}}$的值．