初中数学圆幂定理试题

已知两个圆相切，圆心距为8cm，其中一个圆的半径为12cm，则另一个圆的半径为            ．

在学校组织的实践活动中，小新同学用纸板制作了一个圆锥模型，它的底面半径为1，高为，则这个圆锥的侧面积是

A．4π

B．3π

C．π

D．2π

如图，半径为5cm的圆中，圆心到弦AB的距离OE的长为4cm，则弦AB的长是

A．3cm

B．4cm

C．5cm

D．6cm

如图，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E，若∠AOD=60°，则∠DBC的度数为

A．30°

B．40°

C．50°

D．60°

如图，在扇形OAB中，半径OA=4，∠AOB=120°，点C在上，OD⊥AC于点D，OE⊥BC于点E，当点C从点A运动到点B时，线段DE长度的变化情况是（   ）

A．先变小，后变大

B．先变大，后变小

C．DE与OD的长度保持相等

D．固定不变

如果所在圆的半径为3cm，它所对圆心角的度数是120°,那么的长是（   ）cm．

A．

B．

C．

D．

如图，CD垂直平分半径OB，垂足为P点，CD＝12，则OB=（    ）

A．

B．

C．

D．

如图，点A，B，C是⊙O上的三点，∠AOC＝110°，则∠ABC等于（     ）

A．70°

B．65°

C．55°

D．50°

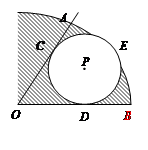
如图，在Rt△ABC中，∠ACB=90°，AC=6，D为BC边上一点，CD=3，过A，C，D三点的⊙O与斜边AB交于点E，连结DE．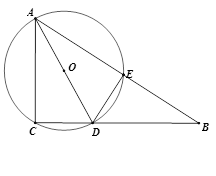

（1）求证：△BDE ∽△BAC；
（2）求△ACD外接圆的直径的长；
（3）若AD平分∠CAB，求出BD的长．

如图，点A，B，C，D在⊙O上，且AB=CD，求证：CE=BE．

如图、矩形ABCD中，AB=8，AD=6．点M是对角线AC上的一个动点，以M点为圆心，线段AM长为半径画一个⊙M，若⊙M在以C为端点的矩形ABCD边上截得的线段EF=AM，则线段AM的长是                ．

如图，点C，D是半圆O的三等分点，直径AB=．连结AC交半径OD于E，则线段DE，CE以及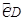围成的封闭图形（即阴影部分）的面积是         ．

如图，点A，B，C在⊙O上，AO∥BC，∠OAC=25°，则∠AOB的度数是          度．

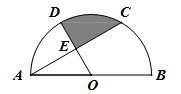
如图，⊙P与扇形OAB的半径OA、OB分别相切于点C、D，与弧AB相切于点E,已知OA=15cm，∠AOB=60°，求图中阴影部分的面积．

已知：如图，以的边为直径的交边于点，且过 点的切线平分边．

（1）求证：是的切线；
（2）当满足什么条件时，以点、、、 为顶点的四边形是平行四边形？请说明理由．