初中数学圆幂定理试题

如图，直线AB、CD相交于点O，∠AOC=30⁰，半径为1cm的⊙P的圆心在射线OA上，开始时，PO=6cm．如果⊙P以1cm/秒的速度沿由A向B的方向移动，那么当⊙P的运动时间t（秒）满足         条件时，⊙P与直线CD相交． 

已知圆锥的底面半径为40cm，母线长为90cm，则它的侧面展开图的圆心角为         ．

⊙O的直径为10，弦AB的长为8，M是弦AB上的动点，则OM的长的取值范围

A．3≤OM≤5	B．4≤OM≤5
C．3＜OM＜5	D．4＜OM＜5

如图，在平面直角坐标系中，⊙A与x轴相交于C（﹣2，0），D（﹣8，0）两点，与y轴相切于点B（0，4）．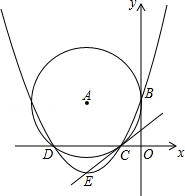

（1）求经过B，C，D三点的抛物线的函数表达式；
（2）设抛物线的顶点为E，证明：直线CE与⊙A相切；
（3）在x轴下方的抛物线上，是否存在一点F，使△BDF面积最大，最大值是多少？并求出点F的坐标．

已知：如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点P，PD⊥AC于点D．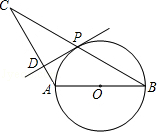

（1）求证：PD是⊙O的切线；
（2）若∠CAB=120°，AB=2，求BC的值．

如图，一条公路的转弯处是一段圆弧AB．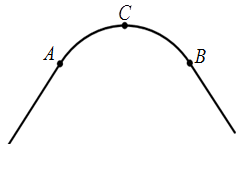

（1）用直尺和圆规作出弧AB所在圆的圆心O；（要求保留作图痕迹，不写作法）
（2）若弧AB的中点C到弦AB的距离为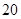m，AB＝80m，求弧AB所在圆的半径．

如图，已知C是弧AB的中点，OC交弦AB于点D．∠AOB=120°，AB=．
求OA的长。

如图，正六边形ABCDEF的边长为2cm，点P为六边形内任一点．则点P到各边距离之和为        cm．

如图，PA、PB切⊙O于点A、B，点C是⊙O上一点，且∠ACB=65°，则∠P=       度．

如图，两同心圆的圆心为O，大圆的弦AB切小圆于P，两圆的半径分别为6，3，则图中阴影部分的面积是（   ）

A．

B．

C．

D．

如右图，内接于⊙O，，，是⊙O的直径，BD交AC于点E，连结DC，则等于（   ）

A．70°

B．110°

C．90°

D．120°

在平面直角坐标系中，以点（2，3）为圆心，2为半径的圆必定（ ）

A．与x轴相离，与y轴相切

B．与x轴， y轴都相离

C．与x轴相切，与y轴相离

D．与x轴，y轴都相切

过⊙O内一点M的最长弦为10 cm，最短弦长为8cm，则OM的长为（  ）

A．9cm

B．6cm

C．3cm

D．

如图，已知⊙O的直径AB=12cm，AC是⊙O的弦，过点C作⊙O的切线交BA的延长线于点P，连接BC．

（1）求证：∠PCA=∠B；
（2）已知∠P=40°，点Q在优弧ABC上，从点A开始逆时针运动到点C停止（点Q与点C不重合），当△ABQ与△ABC的面积相等时，求动点Q所经过的弧长．

如图，已知AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，∠M=∠D．

（1）判断BC、MD的位置关系，并说明理由；
（2）若AE=16，BE=4，求线段CD的长；
（3）若MD恰好经过圆心O，求∠D的度数．