(本题10分)
AB为⊙O的直径,CD与⊙O相切于点C,且OD⊥BC,垂足为F,OD交⊙O于E点
(1)证明:

(2)∠D=∠AEC;
(3)若⊙O的半径为5,BC=8,求⊿CDE的面积。
如图,在ΔABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是 。
如图,如果从半径为9cm的圆形纸片剪去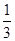 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ㎝。
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ㎝。
如图四边形ABCD内接于⊙O,AB为直径,PD切⊙O于D,与BA延长线交于P点,已知∠BCD=130º,则∠ADP= .

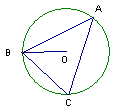
如图所示, ⊙O是△ABC的外接圆,已知∠ABO= 20º,则∠C的度数为( )
| A.45º | B.60º | C.70º | D.90º |
已知:如图, ,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1cm,则这个圆锥的底面半径为( )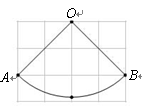
A.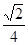 cm cm |
B.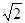 cm cm |
C.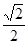 cm cm |
D.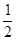 cm cm |
如图,点A在半径为3的⊙O内,OA= ,P为⊙O上一点,
,P为⊙O上一点,
当∠OPA取最大值时,PA的长等于( ).
A. |
B. |
C.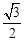 |
D. |
如图,以原点为圆心的圆与反比例函数 的图象交于
的图象交于 、
、 、
、 、
、 四点,已知点
四点,已知点 的横坐标为1,则点
的横坐标为1,则点 的横坐标( )
的横坐标( )
A. |
B. |
C. |
D. |
如图,圆锥的轴截面 是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径
是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径 =" 4" cm,母线
=" 4" cm,母线 =" 6" cm,则由点
=" 6" cm,则由点 出发,经过圆锥的侧面到达母线
出发,经过圆锥的侧面到达母线 的最短路程是( )
的最短路程是( )
A. cm cm |
B.6cm | C. cm cm |
D. cm cm |
(本题满分12分) 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.

(1)求证:PC是⊙O的切线;
(2)求∠P的度数;
(3)点M是弧AB的中点,CM交AB于点N,AB=4,求线段BM、CM及弧BC所围成的图形面积。
如图, ,半径为1cm的圆O切BC于点C,若将圆O在CB上向右滚动,则当滚动到圆O与CA也相切时,圆心O移动的水平距离是__________cm.
,半径为1cm的圆O切BC于点C,若将圆O在CB上向右滚动,则当滚动到圆O与CA也相切时,圆心O移动的水平距离是__________cm.
已知圆锥的底面半径长为5,侧面展开后所得的扇形的圆心角为120°,则该圆锥的母线长等于______________。
( 10分)如图,已知点 ,经过A、B的直线
,经过A、B的直线 以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线
以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线 上以每秒1个单位的速度沿直线
上以每秒1个单位的速度沿直线 向右下方向作匀速运动.设它们运动的时间为
向右下方向作匀速运动.设它们运动的时间为 秒.
秒.
(1)用含
 的代数式表示点P的坐标;
的代数式表示点P的坐标;(2)过O作OC⊥AB于C,过C作CD⊥
 轴于D,问:
轴于D,问: 为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时
为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时 与直线CD的位置关系.
与直线CD的位置关系.