初中数学圆幂定理试题

．小明用一个半径为5，面积为15的扇形纸片，制作成一个圆锥的侧面（接缝处不重叠），那么这个圆锥的底面半径为

A．3

B．4

C．5

D．15

．如图，A，D是⊙上的两个点，BC是直径，若∠D = 35°，则∠OAC的度数是

A．35°

B．55°

C．65°

D．70°

．
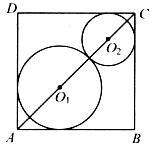
如图，在正方形ABCD内，已知两个动圆⊙O₁与⊙Q₂互相外切．且⊙O₁与边AB，AD相切，⊙O₂与边BC，CD相切，若正方形的边长为1，⊙O₁与⊙Q₂的半径分别为，．

（1）求和的关系式；
（2）求⊙O₁与⊙Q₂的面积之和的最小值．

如图，AC为⊙O直径，B为AC延长线上的一点，BD交⊙O于点D，
∠BAD=∠B=30°．

（1）求证：BD是⊙O的切线；
（2）AB=3CB吗?请说明理由．

如图，已知⊙O的半径为2，圆心在坐标原点，AC，BD为⊙O的两条相互垂直的弦，垂足为M（1，），且AC⊥轴，BD⊥轴．则四边形ABCD的面积为______________．

如图是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF长为10cm．母线OE（OF）长为10cm．在母线OF上的点A处有一块爆米花残渣，且FA=2cm，一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点，则此蚂蚁爬行的最短距离为____________cm．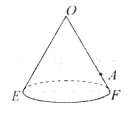

如图，⊙O是△ABC的内切圆，切点分别是D、E、F，已知∠A=110°，则∠DEF的度数是（   ）

A．35°                        B．40°                        C．45°                              D．70°

如图，在中，，以AB为直径的交BC
于点D，DE⊥AC于点E．

求证DE是的切线；
若∠BAC=120°，AB=2，求△DEC的面积．

已知是半径为1的⊙的一条弦，且．以弦为一边在⊙内作
正△，点为⊙上不同于点A的一点，且，的延长线交
⊙于点，则的长为（ ▲ ）．
A．      B．1    C．     D．

两圆的半径分别为3和5，圆心距为7，则两圆的位置关系是（ ▲ ）
A．相交        B.内切       C.外切        D.外离

已知：如图，⊙O为的外接圆，为⊙O的直径，作射线，使得平分，过点作于点.

(1)求证：为⊙O的切线；
(2)若，，求⊙O的半径.

如图，⊙O₁和⊙O₂的半径为2和3，连接O₁O₂，交⊙O₂于点P，O₁O₂=7，若将⊙O₁绕点按顺时针方向以30°/秒的速度旋转一周，请写出⊙O₁与⊙O₂相切时的旋转时间为_______秒．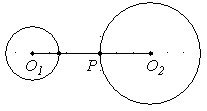

已知圆锥的母线长为5，底面半径为3，则圆锥的表面积为（   ）

A．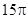

B．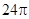

C．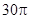

D．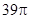

如图，⊙O的直径AB＝4，C、D为圆周上两点，且四边形OBCD是菱形，过点D的直线EF∥AC，交BA、BC的延长线于点E、F．

（1）求证：EF是⊙O的切线；
（2）求DE的长．

如图，⊙O的直径AB＝4，BC切⊙O于点B，OC平行于弦AD，OC＝5，则AD的长为（      ）

A．     B．    C． 　 D．