[山东]2011年山东省东营市学业水平模拟考试数学卷
甲型H1N1流感病毒的直径约为0.08微米至0.12微米,普通纱布或棉布口罩不能阻挡甲型H1N1流感病毒的侵袭,只有配戴阻隔直径低于0.075微米的标准口罩才能有效.0.075微米用科学记数法表示正确的是( )
A.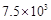 微米 微米 |
B.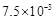 微米 微米 |
C. 微米 微米 |
D. 微米 微米 |
抛物线y=3(x-1) +1的顶点坐标是( )
+1的顶点坐标是( )
| A.(1,1) | B.(-1,1) | C.(-1,-1) | D.(1,-1) |
如图,由四个相同的直角三角板拼成的图形,设三角板的直角边分别为 、
、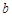 (
(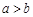 ),则这两个图形能验证的式子是( )
),则这两个图形能验证的式子是( )
A. |
B. |
C. |
D. |
如图,一个由若干个相同的小正方体堆积成的几何体,它的主视图、左视图和俯视图都是田字形,则小正方体的个数是( )
| A.6、7或8 | B.6 | C.7 | D.8 |
如图,圆锥的轴截面 是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径
是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径 =" 4" cm,母线
=" 4" cm,母线 =" 6" cm,则由点
=" 6" cm,则由点 出发,经过圆锥的侧面到达母线
出发,经过圆锥的侧面到达母线 的最短路程是( )
的最短路程是( )
A. cm cm |
B.6cm | C. cm cm |
D. cm cm |
张老师上班途中要经过3个十字路口,每个十字路口遇到红、绿灯的机会都相同,张老师希望上班经过每个路口都是绿灯,但实际上这样的机会是( )
A. |
B. |
C. |
D. |
有30位同学参加数学竞赛,已知他们的分数互不相同,按分数从高到低选l5位同 学进入下一轮比赛.小明同学知道自己的分数后,还需知道哪 个统计量,才能判断自己能否进入下一轮比赛?
个统计量,才能判断自己能否进入下一轮比赛?
| A.众数 | B.方差 | C.中位数 | D.平均数 |
如图,以原点为圆心的圆与反比例函数 的图象交于
的图象交于 、
、 、
、 、
、 四点,已知点
四点,已知点 的横坐标为1,则点
的横坐标为1,则点 的横坐标( )
的横坐标( )
A. |
B. |
C. |
D. |
两个完全相同的三角形纸片,在平面直角坐标系中的摆放位置如图所示,点P与点 是一对对应点,若点P的坐标为(
是一对对应点,若点P的坐标为( ,
, )则点
)则点 的坐标为( )
的坐标为( )
A.( ,
, ) B. (
) B. ( ,
, )C(
)C( ,
, ). D.(
). D.( ,
, )
)
若方程x2-3x-2=0的两实根为x1、x2,则(x1+2)(x2+2)的值为 ( )
| A.-4 | B.6 | C.8 | D.12 |
如图 ,过
,过 上到点
上到点 的距离分别为
的距离分别为 的点作
的点作 的垂线与
的垂线与 相交,得到并标出一组黑色梯形,它们的面积分别为
相交,得到并标出一组黑色梯形,它们的面积分别为 .观察图中的规律,求出第10个黑色梯形的面积
.观察图中的规律,求出第10个黑色梯形的面积 ( )
( )
| A.32 | B.54 | C.76 | D.84 |
如图,在平面直角坐标系中,矩形 的边与坐标轴平行或垂直,顶点
的边与坐标轴平行或垂直,顶点 、
、 分别在函数
分别在函数 的图象的两支上,则图中两块阴影部分的面积的乘积等于__________.
的图象的两支上,则图中两块阴影部分的面积的乘积等于__________.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径 、
、 交于点
交于点 ,半径
,半径 、
、 交于点
交于点 ,且点
,且点 是弧AB的中点,若扇形的半径为2,则图中阴影部分的面积等于____________________.
是弧AB的中点,若扇形的半径为2,则图中阴影部分的面积等于____________________.
“知识改变命运,科技繁荣祖国”.我区中小学每年都要举办一届科技比赛.下图为我区某校2010年参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图:
(1)该校参加机器人、建模比赛的人数分别是 人和 人;
(2)该校参加
 科技比赛的总人数是 人,电子百拼所在扇形的圆心角的度数
科技比赛的总人数是 人,电子百拼所在扇形的圆心角的度数 是 °,并把条形统计图补充完整;
是 °,并把条形统计图补充完整; (3)从全区中小学参加科技比赛选手中随机抽取80人,其中有32人获奖. 今年我区中小学参加科技比赛人数共有24
 85人,请你估算今年参加科技比赛的获奖人数约是多少人?
85人,请你估算今年参加科技比赛的获奖人数约是多少人?
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE上AC,垂足为E。
(1)求证:DE为⊙O的切线;
(2)若⊙O的半径为5,∠BAC=60°,求DE的长.
如图,小丽家住在成都市锦江河畔的电梯公寓AD内,她家河对岸新建了一座大厦BC,为了测得大厦的高度,小丽在她家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大顶部B的仰角为30°,已知小丽所住的电梯公寓高82米,请你帮助小丽算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。
如图,在平面直角坐标系中,直线 分别与
分别与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,
, 的平分线交
的平分线交 轴于点
轴于点 ,点
,点 在线段
在线段 上,以
上,以 为直径的⊙D经过点
为直径的⊙D经过点 .
.
⑴ 判断⊙D与
 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;⑵ 求点
 的坐标.
的坐标.
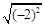 的平方根是( )
的平方根是( )



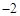
 的正比例函数的表达式为____________.
的正比例函数的表达式为____________. =_____________________________.
=_____________________________. 、
、 在以
在以 为直径的半圆上,
为直径的半圆上, ,若
,若 的长为________________.
的长为________________.
 5分,共10分)
5分,共10分) .
. 如图,已知关于
如图,已知关于 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 、
、 两点(点
两点(点 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
 点
点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 的函数关系式,并写出
的函数关系式,并写出 粤公网安备 44130202000953号
粤公网安备 44130202000953号