初中数学圆幂定理填空题

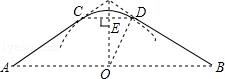
如图，某公园的一角有一块草坪（阴影部分），实线部分是沿草坪外围的一条小路，小路由两条相等的线段AC、BD和圆弧CD组成，其中AC、BD分别与圆弧CD相切于点C、D．经过测量，线段CD与半径OD都为60米，则这条小路的长度为          米．

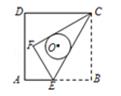
如图，正方形ABCD的边长为6，点E是AB上的一点，将△BCE沿CE折叠至△FCE，若CF，CE恰好与以正方形ABCD的中心为圆心的⊙O相切，则折痕CE=  ________．

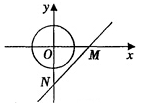
如图，直线与坐标轴交于AB两点，点是轴上一动点，以点M为圆心，2个单位长度为半径作⊙M，当⊙M与直线想切时，的值为__________________．

如图，正六边形ABCDEF的边长为2cm，点P为六边形内任一点．则点P到各边距离之和为        cm．

在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结PA，PB。若PB=4，则PA的长为   ．

如图，直线y＝x－2与x轴、y轴分别交于M、N两点，现有半径为1的动圆圆心位于原点处，并以每秒1个单位的速度向右作平移运动．已知动圆在移动过程中与直线MN有公共点产生，当第一次出现公共点到最后一次出现公共点，这样一次过程中该动圆一共移动    秒．

如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点，若⊙O的半径为7，则GE+FH的最大值为                ．

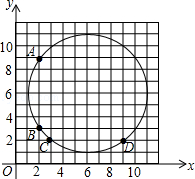
在如图所示的平面直角坐标系中，点A（2，9），B（2，3），C（3，2），D（9，2）在⊙P上，则圆心P的坐标是      ．

如图，扇形OMN与正三角形ABC，半径OM与AB重合，扇形弧MN的长为AB的长，已知AB=10，扇形沿着正三角形翻滚到首次与起始位置相同，则点O经过的路径长       ．

如图，⊙I为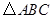的内切圆，点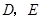分别为边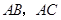上的点，且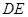为⊙I的切线，若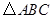的周长为21，边的长为6，则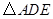的周长为（ ）．

A．15

B．8

C．9

D．7．5

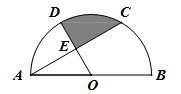
如图，点C，D是半圆O的三等分点，直径AB=．连结AC交半径OD于E，则线段DE，CE以及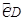围成的封闭图形（即阴影部分）的面积是         ．

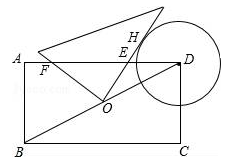
如图，在矩形ABCD中，AB=2，BC=4，⊙D的半径为1．现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则EH的值为           ．

已知△ABC内接于⊙O，过点A作直线EF．

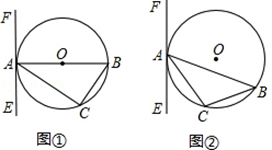
（1）如图①所示，若AB为⊙O的直径，要使EF成为⊙O的切线，还需要添加的一个条件是（至少说出两种）：       或者       ．
（2）如图②所示，如果AB是不过圆心O的弦，且∠CAE=∠B，那么EF是⊙O的切线吗？试证明你的判断．

由“不在同一直线上的三点确定一个圆”，可以判断平面直角坐标系内的三个点A（3，0）、B（0，﹣4）、C（2，﹣3）                确定一个圆（填“能”或“不能”）．

如图，点P在双曲线y=（x>0）上，OP与两坐标轴都相切，点E为y轴负半轴上的一点，过点P作PF⊥PE交x轴于点F，若OF-OE=6，则k的值是____．