初中数学圆幂定理解答题

如图1，AB为⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE=CB．

（1）求证：BC为⊙O的切线；
（2）连结AE并延长，交BC的延长线于点G（如图2所示），若AB=2，AD=2，求线段BC和EG的长．

如图，⊙O是△ABC的外接圆，AB是直径，过点O作OD⊥CB，垂足为点D，延长DO交⊙O于点E，过点E作PE⊥AB，垂足为点P，作射线DP交CA的延长线于F点，连接EF，

（1）求证：OD=OP；
（2）求证：FE是⊙O的切线．

如图，已知△ABC内接于⊙O，点D在OC的延长线上，∠ABC＝∠CAD．

（1）若∠ABC＝20°，则∠OCA的度数为   ；
（2）判断直线AD与⊙O的位置关系，并说明理由；
（3）若OD⊥AB，BC＝5，AB＝8，求⊙O的半径．

已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D．

（Ⅰ）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；
（Ⅱ）如图②，若∠CAB=60°，求BD的长．

如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．

（1）试说明四边形EFCG是矩形；
（2）当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，
①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；
②求点G移动路线的长．

如图，在△ABC中，AB＝AC，以AB为直径作⊙O，交BC边于点D，交AC边于点G，过D作⊙O的切线EF，交AB的延长线于点F，交AC于点E。

（1）求证：BD=CD
（2）若AE＝6，BF＝4,求⊙O的半径；
（3）在（2）条件下判断△ABC的形状，并说明理由；

问题提出:
平面内不在同一条直线上的三点确定一个圆．那么平面内的四点（任意三点均不在同一直线上），能否在同一个圆呢？
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O．
（1）当C、D在线段AB的同侧时，
如图①，若点D在⊙O上，此时有∠ACB=∠ADB，理由是               ；
如图②，若点D在⊙O内，此时有∠ACB   ∠ADB；
如图③，若点D在⊙O外，此时有∠ACB   ∠ADB．（填“=”、“＞”或“＜”）；

由上面的探究，请直接写出A、B、C、D四点在同一个圆上的条件：          ．
类比学习
（2）仿照上面的探究思路，请探究：当C、D在线段AB的异侧时的情形．

此时有            ， 此时有             ， 此时有             ．
由上面的探究，请用文字语言直接写出A、B、C、D四点在同一个圆上的条件： ． 
拓展延伸
（3）如何过圆上一点，仅用没有刻度的直尺，作出已知直径的垂线？
已知：如图，AB是⊙O的直径，点C在⊙O上．
求作：CN⊥AB．
作法：①连接CA，CB；
②在上任取异于B、C的一点D，连接DA，DB；
③DA与CB相交于E点，延长AC、BD，交于F点；
④连接F、E并延长，交直径AB于M；
⑤连接D、M并延长，交⊙O于N．连接CN．
则CN⊥AB．
请按上述作法在图④中作图，并说明CN⊥AB的理由．（提示：可以利用（2）中的结论）

如图,在□ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE．

（1）判断四边形ABED的形状，并说明理由；
（2）判断直线DC与⊙O的位置关系，并说明理由；
（3）若AB=3，AE=6，求CE的长．

如图，AB为⊙O的直径，M为⊙O外一点，连接MA与⊙O交于点C，连接MB并延长交⊙O于点D，经过点M的直线l与MA所在直线关于直线MD对称．作BE⊥l于点E，连接AD，DE．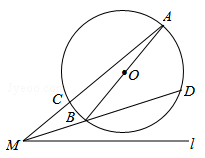

（1）依题意补全图形；
（2）在不添加新的线段的条件下，写出图中与∠BED相等的角，并加以证明．

如图，AB是⊙O的直径，CD是⊙O的切线，切点为C，BE⊥CD，垂足为E，连接AC、BC．

（1）判断△ABC的形状并说明理由；
（2）求证：BC平分∠ABE；
（3）若∠A＝60°，OA＝2，求CE的长．

如图，正方形ABCD中，以BC为直径作半圆，BC=2㎝．现有两动点E、F，分别从点B、点A同时出发，点E沿线段BA以/秒的速度向点A运动，点F沿折线A→D→C以/秒的速度向点C运动．当点E到达A点时，E、F同时停止运动，设点E运动时间为．

（1）当为何值时，线段EF与BC平行？
（2）设，当为何值时，EF与半圆相切？
（3）如图2，将图形放在直角坐标系中，当时，设EF与AC相交于点P，双曲线经过点P，并且与边AB交于点H，求出双曲线的函数关系式，并直接写出的值．

如图，CD是⊙O的直径，且CD=2㎝，点P为CD的延长线上一点，过点P作⊙O的切线PA、PB，切点分别为A、B．

（1）连接AC，若∠APO=30°，试证明△ACP是等腰三角形；
（2）填空：①当DP= 时，四边形AOBD是菱形；
②当DP= 时，四边形PAOB是正方形．

已知：如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．

（1）求证：AE与⊙O相切；
（2）当BC=4，cosC=时，求⊙O的半径．

对于半径为r的⊙P及一个正方形给出如下定义：若⊙P上存在到此正方形四条边距离都相等的点，则称⊙P是该正方形的“等距圆”．如图1，在平面直角坐标系xOy中，正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧．
（1）当r=时，
①在P₁（0，-3），P₂（4，6），P₃（，2）中可以成为正方形ABCD的“等距圆”的圆心的是_______________；
②若点P在直线上，且⊙P是正方形ABCD的“等距圆”，则点P的坐标为_______________；
（2）如图2，在正方形ABCD所在平面直角坐标系xOy中，正方形EFGH的顶点F的坐标为（6，2），顶点E、H在y轴上，且点H在点E的上方．
①若⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，求⊙P 在y轴上截得的弦长；
②将正方形ABCD绕着点D旋转一周，在旋转的过程中，线段HF上没有一个点能成为它的“等距圆”的圆心，则r的取值范围是_______________                ．

如图1，在平面直角坐标系中，直线的位置随b的不同取值而变化．
（1）已知⊙M的圆心坐标为（4，2），半径为2，
①当b=               时，直线经过圆心M ；
②当b=               时，直线与 ⊙M相切；
（2）若把⊙M换成矩形ABCD，如图2，其三个顶点的坐标分别为：A（2，0），B（6，0），C（6，2）．设直线l扫过矩形ABCD的面积为S，当b由小到大变化时，请求出S与b的函数关系式．