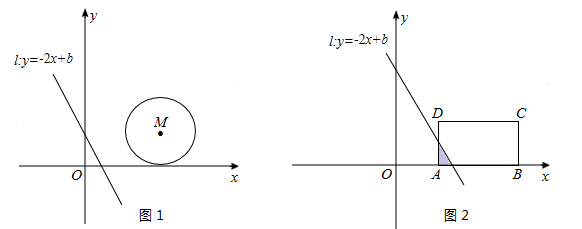如图1,在平面直角坐标系中,直线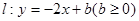 的位置随b的不同取值而变化.
的位置随b的不同取值而变化.
(1)已知⊙M的圆心坐标为(4,2),半径为2,
①当b= 时,直线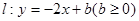 经过圆心M ;
经过圆心M ;
②当b= 时,直线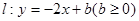 与 ⊙M相切;
与 ⊙M相切;
(2)若把⊙M换成矩形ABCD,如图2,其三个顶点的坐标分别为:A(2,0),B(6,0),C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.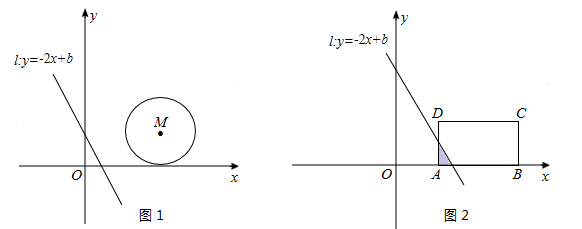
相关知识点
推荐套卷
如图1,在平面直角坐标系中,直线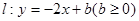 的位置随b的不同取值而变化.
的位置随b的不同取值而变化.
(1)已知⊙M的圆心坐标为(4,2),半径为2,
①当b= 时,直线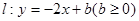 经过圆心M ;
经过圆心M ;
②当b= 时,直线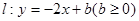 与 ⊙M相切;
与 ⊙M相切;
(2)若把⊙M换成矩形ABCD,如图2,其三个顶点的坐标分别为:A(2,0),B(6,0),C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.