如图，正方形ABCD中，以BC为直径作半圆，BC=2㎝．现有两动点E、F，分别从点B、点A同时出发，点E沿线段BA以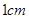
/秒的速度向点A运动，点F沿折线A→D→C以
/秒的速度向点C运动．当点E到达A点时，E、F同时停止运动，设点E运动时间为
．
（1）当为何值时，线段EF与BC平行？
（2）设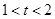
，当为何值时，EF与半圆相切？
（3）如图2，将图形放在直角坐标系中，当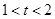时，设EF与AC相交于点P，双曲线
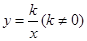经过点P，并且与边AB交于点H，求出双曲线的函数关系式，并直接写出
的值．
如图1，在平面直角坐标系中，抛物线与 轴分别交于 、 两点，与 轴交于点 ，抛物线的顶点坐标为 ，连结 、 、 ．
（1）求抛物线的表达式；
（2）判断 的形状，并说明理由；
（3）如图2，以 为圆心， 为半径作 ，在 上是否存在点 ，使得 的值最小，若存在，请求出最小值；若不存在，请说明理由．
如图1， 为 上一点，点 在直径 的延长线上，且 ．
（1）判断直线 与 的位置关系，并说明理由；
（2）若 ， ，求 的半径；
（3）如图2，在（2）的条件下， 的平分线 交 于点 ，交 于点 ，连结 ．求 的值．
如图，一次函数 的图象与反比例函数 的图象交于点 、 ，与 轴交于点 ，若 ，且 ．
（1）求反比例函数与一次函数的表达式；
（2）请直接写出不等式 的解集．
全国历史文化名城宜宾有许多名胜古迹，始建于明朝的白塔是其中之一．如图，为了测量白塔的高度 ，在 处测得塔顶 的仰角为 ，再向白塔方向前进15米到达 处，又测得塔顶 的仰角为 ，点 、 、 在同一水平线上，求白塔的高度 ． ，精确到1米）
粤公网安备 44130202000953号