初中数学圆幂定理解答题

如图，已知⊙O的半径为1，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．
（1）求AD的长；
（2）BC是⊙O的切线吗？若是，给出证明；若不是，说明理由．

如图所示，AB是⊙O的弦，D为OA半径的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB．

（1）求证：BC是⊙O的切线；
（2）连接AF，BF，求∠ABF的度数；
（3）如果CD=15，BE=10，sinA=，求⊙O的半径

如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的直线互相垂直，垂足为D，且AC平分∠DAB．
（1）求证：DC为⊙O的切线；
（2）若⊙O的半径为3，AD="4" ，求AC的长．

如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5．OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．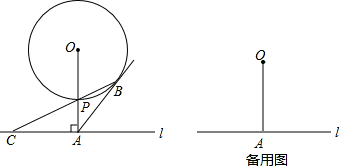

（1）试判断线段AB与AC的数量关系，并说明理由；
（2）若PC=2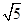，求⊙O的半径和线段PB的长；
（3）若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，求⊙O的半径r的取值范围．

如图，在△ABC中，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且AC=CF，∠CBF=∠CFB．
（1）求证：直线BF是⊙O的切线；
（2）若点D，点E分别是弧AB的三等分点，当AD=5时，求BF的长；
（3）填空：在（2）的条件下，如果以点C为圆心，r为半径的圆上总存在不同的两点到点O的距离为5，则r的取值范围为             ．

如图，AB是⊙O的直径，C、D在⊙O上，连结BC，过D作PF∥AC交AB于E，交⊙O于F，交BC于点G，交过B点的直线于点P，且∠BPF=∠ADC．

（1）判断直线BP与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为，AC=2，BE=1，求BP的长．

已知：点D是等腰直角三角形ABC斜边BC所在直线上一点（不与点B重合），连接AD．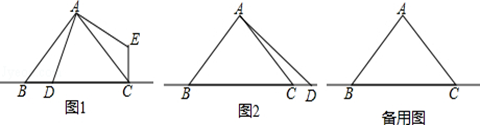

（1）如图1，当点D在线段BC上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．求证：BD=CE，BD⊥CE．
（2）如图2，当点D在线段BC延长线上时，探究AD、BD、CD三条线段之间的数量关系，写出结论并说明理由；
（3）若BD=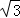CD，直接写出∠BAD的度数．

如图，在直角坐标系中，已知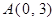、、、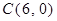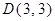，点P从C点出发，沿着折线C﹣D﹣A运动到达点A时停止，过C点作直线GC⊥PC，且与过O、P、C三点的⊙M交于点G，连接OP、PG、OD．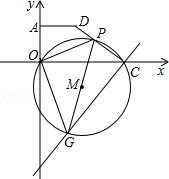

（1）直接写出∠DCO的度数；
（2）当点P在线段CD上运动时，求△OPG的最小面积；
（3）设圆心M的纵坐标为n，试探索：在点P运动的整个过程中，n的取值范围．

如图所示，已知圆锥底面半径r=10cm，母线长为40cm．

（1）求它的侧面展开图的圆心角；
（2）若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B，求它所走的最短路线。

如图，在平面直角坐标系中，⊙A与x轴相交于C（﹣2，0），D（﹣8，0）两点，与y轴相切于点B（0，4）．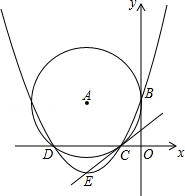

（1）求经过B，C，D三点的抛物线的函数表达式；
（2）设抛物线的顶点为E，证明：直线CE与⊙A相切；
（3）在x轴下方的抛物线上，是否存在一点F，使△BDF面积最大，最大值是多少？并求出点F的坐标．

如图，矩形OACB，A（0，3）、B（6，0），点E在线段OB上，∠AEO=30°，点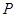从点Q（-4，0）出发，沿x轴向右以每秒1个单位长度的速度运动，运动时间为t秒．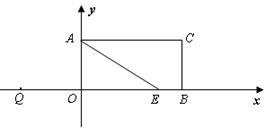

（1）求点E的坐标；
（2）当∠PAE=15°时，求t的值；
（3）以点P为圆心，PA为半径的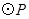随点P的运动而变化，当与四边形AEBC的边（或边所在的直线）相切时，求t的值．

如图，半圆O的直径DE＝12cm，Rt△ABC中，∠ACB＝90°，∠ABC＝30°，BC＝12cm．半圆O以2cm/s的速度从左向右运动，在运动过程中，直径DE始终在直线BC上．设运动时间为t（s），当t＝0（s）时，半圆O在△ABC的左侧，OC＝8cm．

（1）外
当t＝8（s）时，试判断点C与半圆O所在的圆的位置关系．
外
（2）当t为何值时，△ABC的一边所在直线与半圆O所在的圆相切．
（3）在（2）的条件下，如果半圆O与△ABC三边围成的区域有重叠部分，求重叠部分的面积．

如图，⊙O的半径为1，直线CD经过圆心O，交⊙O于C、D两点，直径AB⊥CD，点M是直线CD上异于点C、O、D的一个动点，AM所在的直线交于⊙O于点N，点P是直线CD上另一点，且PM=PN．

（1）当点M在⊙O内部，如图一，试判断PN与⊙O的关系，并写出证明过程；
（2）当点M在⊙O外部，如图二，其它条件不变时，（1）的结论是否成立？请说明理由；
（3）当点M在⊙O外部，如图三，∠AMO=30°，求图中阴影部分的面积．

如图，已知等边△ABC，AB=16，以AB为直径的半圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连结GD．

（1）求证：DF是⊙O的切线；
（2）求FG的长；
（3）求tan∠FGD的值．     

学习了勾股定理的逆定理，我们知道：在一个三角形中，如果两边的平方和等于第三边的平方，那么这个三角形为直角三角形．类似地，我们定义：对于任意的三角形，设其三个内角的度数分别为x°、y°和z°，若满足，则称这个三角形为勾股三角形．
（1）根据“勾股三角形”的定义，请你直接判断命题：“直角三角形是勾股三角形”是真命题还是假命题？
（2）已知某一勾股三角形的三个内角的度数从小到大依次为x°、y°和z°，且xy=2160，求x+y的值；
（3）如图，△ABC内接于⊙O，AB=，AC=1+，BC=2，⊙O的直径BE交AC于点D．
①求证：△ABC是勾股三角形；
②求DE的长．