如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )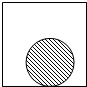
A.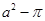 |
B.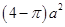 |
C.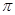 |
D.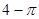 |
如图,矩形ABCD中,AB=4,以点B为圆心,BA为半径画弧交BC于点E,以点O为圆心的⊙O与弧 ,边AD,DC都相切.把扇形BAE作一个圆锥的侧面,该圆锥的底面圆恰好是⊙O,则AD的长为()
,边AD,DC都相切.把扇形BAE作一个圆锥的侧面,该圆锥的底面圆恰好是⊙O,则AD的长为()
| A.4 | B. |
C. |
D.5 |
(11·佛山)若⊙O的一条弧所对的圆周角为60°,则这条弧所对的圆心角是()
| A.30° | B.60° | C.120° | D.以上答案都不对 |
如图,O为原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A、B、O三点,点C为 上一点(不与O、A两点重合),则cosC的值为( )
上一点(不与O、A两点重合),则cosC的值为( )
A. B.
B. C.
C. D.
D.
一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )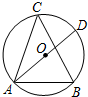
A. |
B.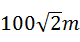 |
C.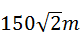 |
D.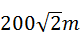 |
如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则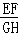 的值是()
的值是()
A.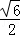 B.
B. C.
C.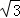 D.2
D.2
如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点 是直线
是直线 上异于A,B的一个动点,且满足
上异于A,B的一个动点,且满足 ,则()
,则()
A.点 一定在射线 一定在射线 上 上 |
B.点 一定在线段 一定在线段 上 上 |
C.点 可以在射线 可以在射线 上,也可以在线段 上,也可以在线段 上 上 |
D.点 可以在射线 可以在射线 上,也可以在线段 上,也可以在线段 上 上 |
如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为( )
A.4 . . |
B.5 |
| C.6. | D.9. |
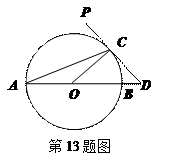
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,
则∠PCA=()
| A.30° | B.45° | C.60° | D.67.5° |
如图3,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB="10,CD=8," 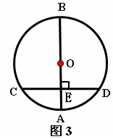
那么线段OE的长为()
| A.5 | B.4 |
| C.3 | D.2 |
如图,直线l:y=-x- 与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合),
与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合),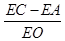 的值是否发生变化?( )
的值是否发生变化?( )
A. |
B.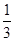 |
C.2 | D.变化 |

圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面积的半径是()
| A.24 | B.12 | C.6 | D.3 |
如图,已知直线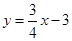 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是()
与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是()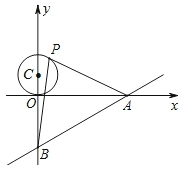
A.8 B.12 C.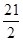 D.
D.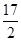
在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为().
A.22 B.24 C.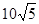 D.
D.