如图,在平面直角坐标系中,分别以点A(2,3),B(3,4)为圆心,以1,3为半径作⊙A,⊙B,点M,N分别是⊙A,⊙B上的动点,P为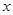 轴上的动点,则PM+PN的最小值为()
轴上的动点,则PM+PN的最小值为()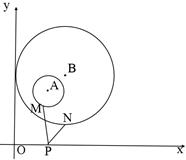
A. |
B.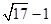 |
C. |
D.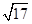 |
圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面积的半径是()
| A.24 | B.12 | C.6 | D.3 |
如图,在半径为6cm的⊙O中, A点是劣弧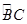 的中点,点D是优弧
的中点,点D是优弧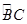 上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论: 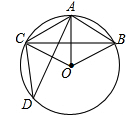
①OA⊥BC;②BC=6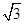 m;③sin∠AOB=
m;③sin∠AOB=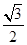 ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.
其中正确结论的序号是()
| A.①③ | B.①②③④ | C.②③④ | D.①③④ |
如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么()秒钟后⊙P与直线CD相切.
A.4 B.8 C.4或6 D.4或8
在平面直角坐标系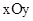 中,直线经过点A(-3,0),点B(0,
中,直线经过点A(-3,0),点B(0,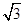 ),点P的坐标为(1,0),与
),点P的坐标为(1,0),与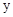 轴相切于点O,若将⊙P沿
轴相切于点O,若将⊙P沿 轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有()
轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有()
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,已知直线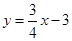 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是()
与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是()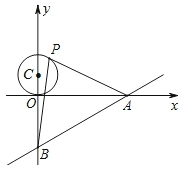
A.8 B.12 C.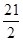 D.
D.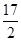
有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴上正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为()
| A.64 | B.52 | C.38 | D.26 |
如图,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中 ,
, ,
, ,…的圆心依次按A,B,C循环.如果AC=1,那么曲线CDEF和线段CF围成图形的面积为( )
,…的圆心依次按A,B,C循环.如果AC=1,那么曲线CDEF和线段CF围成图形的面积为( )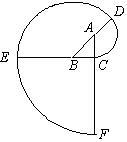
A.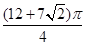 |
B. |
C.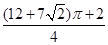 |
D.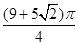 |
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l: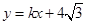 与x轴、y轴分别交于A、B,∠OAB=30º,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是()
与x轴、y轴分别交于A、B,∠OAB=30º,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是()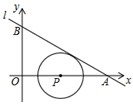
A.6B.8C.10D.12
如图,O为原点,点A的坐标为(3,0),点B的坐标为(0,4),⊙D过A、B、O三点,点C为 上一点(不与O、A两点重合),则cosC的值为( )
上一点(不与O、A两点重合),则cosC的值为( )
A. B.
B. C.
C. D.
D.
如图,O是△ABC的外接圆的圆心,∠ABC=60°,BF,CE分别是AC,AB边上的高且交于点H,CE交⊙O于M,D,G分别在边BC,AB上,且BD=BH,BG=BO,下列结论:①∠ABO=∠HBC;②AB•BC=2BF•BH;③BM=BD;④△GBD为等边三角形,其中正确结论的序号是()
| A.①② | B.①③④ | C.①②④ | D.①②③④ |
如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为()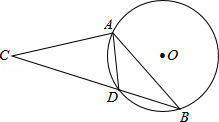
A.2﹣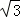 B.
B.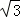 ﹣1 C.2 D.
﹣1 C.2 D.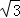 +1
+1
如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则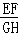 的值是()
的值是()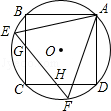
A.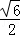 B.
B. C.
C.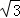 D.2
D.2