如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则cos∠CGD=()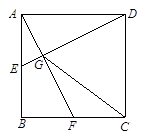
A.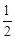 B.
B.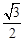 C.
C. D.
D.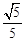
如图,已知矩形ABCD,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示折叠,使点D与点O重合,折痕为FG,点F、G分别在AD,BC上,连接OG、DG,若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是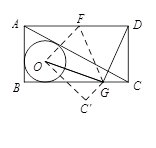
| A.CD+DF="4" | B.CD−DF=2 −3 −3 |
C.BC+AB=2 +4 +4 |
D.BC−AB=2 |
在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为().
A.22 B.24 C.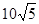 D.
D.
在矩形ABCD中,已知AB=2cm,BC=3cm,现有一根长为2 cm的木棒EF紧贴着矩形的边(即两个端点始终落在矩形的边上),按逆时针方向滑动一周,则木棒EF的中点P在运动过程中所围成的图形的面积为()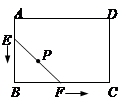
| A.6 cm2 | B.3 cm2 | C.(2+π)cm2 | D.(6-π)cm2 |
在半径为1的⊙O中,弦AB的长为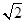 ,则弦AB所对的圆周角的度数为
,则弦AB所对的圆周角的度数为
| A.45° | B.60° | C.45°或135° | D.60°或120° |
如图,在平面直角坐标系 中,直线
中,直线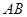 经过点
经过点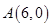 、
、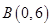 ,⊙
,⊙ 的半径为2(
的半径为2( 为坐标原点),点
为坐标原点),点 是直线
是直线 上的一动点,过点
上的一动点,过点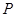 作⊙
作⊙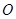 的一条切线
的一条切线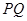 ,
,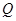 为切点,则切线长
为切点,则切线长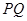 的最小值为().
的最小值为().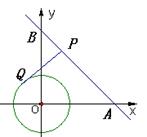
A.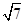 |
B.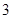 |
C.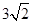 |
D.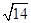 |
如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3,则下列结论不一定成立的是()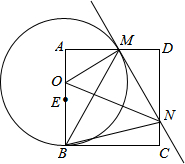
A.S1>S2+S3 B.△AOM∽△DMN C.∠MBN=45° D.MN=AM+CN
如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在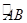 上),则正方形CDEF的边长为()
上),则正方形CDEF的边长为()
| A.3 | B. |
C.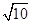 |
D.以上都不正确 |
在平面直角坐标系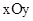 中,直线经过点A(-3,0),点B(0,
中,直线经过点A(-3,0),点B(0,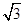 ),点P的坐标为(1,0),与
),点P的坐标为(1,0),与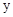 轴相切于点O,若将⊙P沿
轴相切于点O,若将⊙P沿 轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有()
轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有()
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的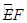 上时,
上时,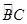 的长度等于( ).
的长度等于( ).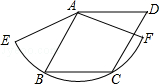
A.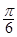 B.
B.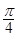 C.
C.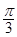 D.
D.
如图,在平面直角坐标系中,分别以点A(2,3),B(3,4)为圆心,以1,3为半径作⊙A,⊙B,点M,N分别是⊙A,⊙B上的动点,P为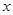 轴上的动点,则PM+PN的最小值为()
轴上的动点,则PM+PN的最小值为()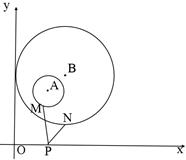
A. |
B.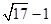 |
C. |
D.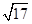 |
小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(1)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(2)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是
A. |
B. |
C. |
D. |
如图,AB是半圆O的直径,点C是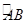 的中点,点D是
的中点,点D是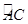 的中点,连接AC.BD交于点E,则
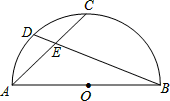
的中点,连接AC.BD交于点E,则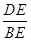 =()
=()
A.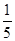 B.
B.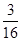 C.
C.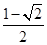 D.
D.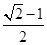
如图,在平面直角坐标系中,过格点A、B、C作一圆弧,则点B与下列格点的连线中,能够与该圆弧相切的是()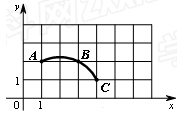
A.点(1,3)B.点(2,3) C.点(4,2) D.点(6,0)