如图,⊙O过点B、C,圆心O在等腰Rt△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为 .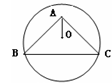
△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是()
| A.80° | B.160° | C.100° | D.80°或100° |
如图,AB为⊙O的弦,C为劣弧AB的中点.
(1)若⊙O的半径为5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断AD与⊙O的位置关系,并说明理由.
如图,以 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦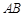 切小圆于点
切小圆于点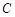 ,若
,若 ,则大圆半径
,则大圆半径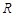 与小圆半径
与小圆半径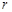 之间满足()
之间满足()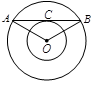
A.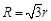 |
B.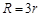 |
C.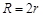 |
D.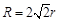 |
一个点到圆上的最小距离是4,最大距离是9,则圆的半径是()
| A.2.5 | B.2.5或6.5 | C.6.5 | D.5或13 |
如图,在直角坐标系中,⊙P的圆心P在x轴上,⊙P与x轴交于点E、F,与y轴交于点C、D,且EO=1,CD=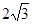 ,又B、A两点的坐标分别为(0,m)、(5,0)
,又B、A两点的坐标分别为(0,m)、(5,0)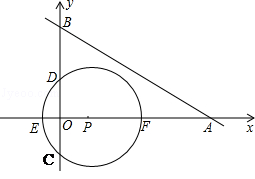
(1)当m=3时,求经过A、B两点的直线解析式;
(2)当B点在y轴上运动时,若直线AB与⊙P保持相交,求m的取值范围.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ,求⊙O的半径。
,求⊙O的半径。