初中数学圆幂定理试题

⊙A半径为5，圆心A的坐标为（1，0），点P的坐标为（-2，4），则点P与⊙A的位置关系是（    ）

A．点P在⊙A上	B．点P在⊙A内
C．点P在⊙A外	D．点P在⊙A上或外

如图，AB是半圆O直径，半径OC⊥AB，连接AC，∠CAB的平分线AD分别交OC于点E，交于点D，连接CD、OD，以下三个结论：
①AC∥OD；②AC＝2CD；③CD²=CE·CO，其中所有正确结论的序号是（   ）

A．①②      B．①③    C．②③         D．①②③

如图，⊙O是△ABC的内切圆，切点分别为D、E、F，点M是⊙O上一点，∠EMF=55°，则∠A=          ．

已知扇形的圆心角为120°，半径为2厘米，则这个扇形的弧长为__________厘米．

如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，若∠PAB=40°，求∠P的度数．

如图，点A（－10，0），B（－6，0），点C在y轴的正半轴上，∠CBO＝45°，CD∥AB，∠CDA＝90°．点P从点Q（8，0）出发，沿x轴向左以每秒1个单位长的速度向点A匀速运动，运动时间为t秒．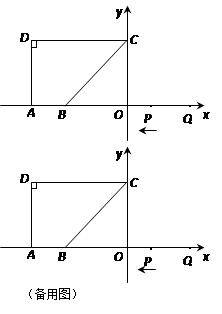

（1）求点C的坐标．
（2）当∠BCP＝15°时，求t的值．
（3）以PC为直径作圆，当该圆与四边形ABCD的边（或边所在的直线）相切时，求t的值．

一个点到圆上的最小距离是4，最大距离是9，则圆的半径是（  ）

A．2．5

B．2．5或6．5

C．6．5

D．5或13

如图，AB是⊙O的直径，AC、DC为弦，∠ACD＝60°，P为AB延长线上的点，∠APD＝30°．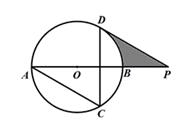

（1）求证：DP是⊙O的切线．
（2）若⊙O的半径为3cm，求图中阴影部分的面积．

如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为（    ）

A．2        B．2        C．2        D．8

如图，在直角坐标系中，⊙P的圆心P在x轴上，⊙P与x轴交于点E、F，与y轴交于点C、D，且EO=1，CD=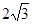，又B、A两点的坐标分别为（0，m）、（5，0）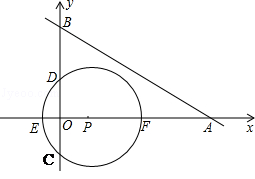

（1）当m=3时，求经过A、B两点的直线解析式；
（2）当B点在y轴上运动时，若直线AB与⊙P保持相交，求m的取值范围．

在圆心角为120°的扇形中，半径为6，则扇形的面积是      ．

直角三角形的两条边长分别为6和8，那么这个三角形的外接圆半径为             

已知圆锥的底面半径为3，侧面积为15，则这个圆锥的高为        ．

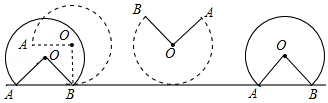
已知一个圆心角为270°扇形工件，未搬动前如图所示，A、B两点触地放置，搬动时，先将扇形以B为圆心，作如图所示的无滑动翻转，再使它紧贴地面滚动，当A、B两点再次触地时停止，半圆的直径为6m，则圆心O所经过的路线长是       m．（结果用含π的式子表示）

如图，∠A是⊙O的圆周角，∠A=50°，则∠BOC的度数为

A．40°

B．50°

C．90°

D．100°