如图,在平面直角坐标系中,点A的坐标为(3,0),直线l与x轴正半轴夹角为30°,点B为直线l上的一个动点,延长AB至点C,使得AB=BC,过点C作CD⊥x轴于点D,交直线l于点F,过点A作AE∥l交直线CD于点E.
(1)若点B的横坐标为6,则点C的坐标为(______,_____),DE的长为 ;
(2)若点B的横坐标大于3,则线段CF的长度是否发生改变?若不变,请求出线段CF的长度;若改变,请说明理由;
(3)连结BE,在点B的运动过程中,以OB为直径的⊙P与△ABE某一边所在的直线相切,请求出所有满足条件的DE的长.
在如图所示的平面直角坐标系中,点A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,则圆心P的坐标是 .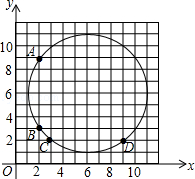
如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),以线段AB为边向上作等边三角形ABC.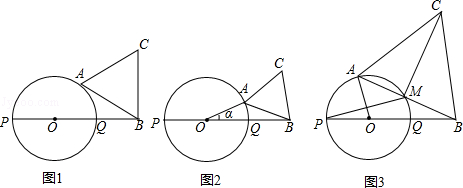
(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1);
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(图3).
如图,已知矩形ABCD,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示折叠,使点D与点O重合,折痕为FG,点F、G分别在AD,BC上,连接OG、DG,若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是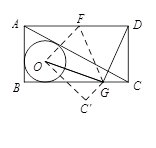
| A.CD+DF="4" | B.CD−DF=2 −3 −3 |
C.BC+AB=2 +4 +4 |
D.BC−AB=2 |
如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20cm,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为 m.(π取3)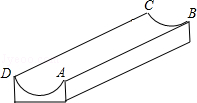
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则EH的值为 .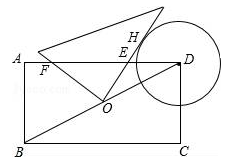
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.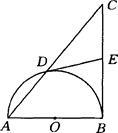
(1)DE与半圆O相切吗?若相切,请给出证明;若不相切,请说明理由;
(2)若AD、AB的长是方程x2-10x+24=0的两个根,求直角边BC的长。
如图,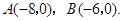 点
点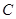 在
在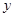 轴的正半轴上,
轴的正半轴上,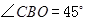 ,
,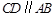 ,
,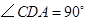 .点
.点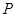 从点
从点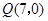 出发,沿
出发,沿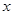 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为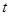 秒.
秒.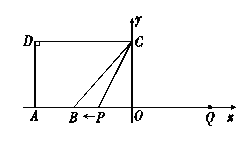
(1)点 的坐标是 ;
的坐标是 ;
(2)当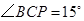 时,求
时,求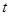 的值;
的值;
(3)以点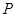 为圆心,
为圆心,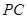 为半径的
为半径的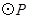 随点
随点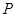 的运动而变化,当
的运动而变化,当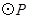 与四边形
与四边形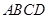 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求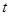 的值.
的值.
若一个三角形的三个顶点均在一个图形的不同的边上,则称此三角形为该图形的内接三角形.
(1)在图①中画出△ABC的一个内接直角三角形;
(2)如图②,已知△ABC中,∠BAC=60°,∠B=45°,AB=8,AD为BC边上的高,探究以D为一个顶点作△ABC的内接三角形,其周长是否存在最小值?若存在,请求出最小值;若不存在,请说明理由;
(3)如图③,△ABC为等腰直角三角形,∠C=90°,AC=6,试探究:△ABC的内接等腰直角三角形的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
如图,在直角坐标系中,已知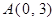 、
、 、
、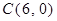 、
、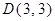 ,点P从C点出发,沿着折线C﹣D﹣A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.
,点P从C点出发,沿着折线C﹣D﹣A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.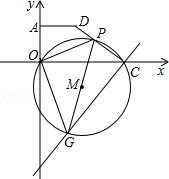
(1)直接写出∠DCO的度数;
(2)当点P在线段CD上运动时,求△OPG的最小面积;
(3)设圆心M的纵坐标为n,试探索:在点P运动的整个过程中,n的取值范围.
如图所示,已知圆锥底面半径r=10cm,母线长为40cm.
(1)求它的侧面展开图的圆心角;
(2)若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,求它所走的最短路线。
如图,点C,D是半圆O的三等分点,直径AB= .连结AC交半径OD于E,则线段DE,CE以及
.连结AC交半径OD于E,则线段DE,CE以及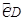 围成的封闭图形(即阴影部分)的面积是 .
围成的封闭图形(即阴影部分)的面积是 .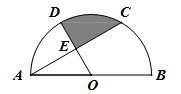
如图,已知☉O的直径AB=8,过A、B两点作☉O的切线AD、BC.
(1)当AD=2,BC=8时,连接OC、OD、CD.
①求△COD的面积.
②试判断直线CD与☉O的位置关系,并说明理由.
(2)若直线CD与☉O相切于点E,设AD=x(x>0),试用含x的式子表示四边形ABCD的面积S,并探索S是否存在最小值,写出探索过程.
如图1,在直角坐标系中,点A的坐标为(1,0),以OA为一边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1,且OD≠2),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形 ;
(2)试说明(1)中找出的损矩形一定有外接圆;
(3)随着点D的位置变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由.
(4)在图2中,过点M作MG⊥y轴,垂足是点G,连结DN,若四边形DMGN为损矩形,求点D的坐标.