.如图,点A、B在⊙O上,直线AC是⊙O的切线,OD⊥OB,连接AB交OC于点D.
⑴求证:AC=CD
⑵若AC=2,AO= ,求OD的长度.
,求OD的长度.
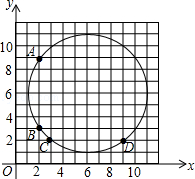
在如图所示的平面直角坐标系中,点A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,则圆心P的坐标是 .
已知圆柱的底面半径为1,母线长为2,则圆柱的侧面积为( )
| A. | 2 | B. | 4 |
| C. | D. |
如图所示,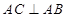 ,
, ,
,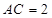 ,点
,点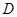 是以
是以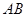 为直径的半圆
为直径的半圆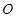 上一动点,
上一动点, 交直线
交直线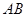 于点
于点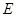 ,设
,设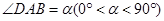 .
.
(1)当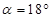 时,求弧BD的长;
时,求弧BD的长;
(2)当 时,求线段
时,求线段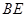 的长;
的长;
(3)若要使点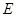 在线段
在线段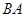 的延长线上,则
的延长线上,则 的取值范围是_________.(直接写出答案)
的取值范围是_________.(直接写出答案)
(本小题满分5分)已知:如图,在 中,
中, ,点
,点 在
在 上,以
上,以 为圆心,
为圆心, 长为半径的圆与
长为半径的圆与 分别交于点
分别交于点 ,且
,且 .
.
(1)判断直线 与
与 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若 ,
, =
= ,求
,求 的值.
的值.
如图,海边有两个灯塔A,B.即将靠岸的轮船得到信息:海里有一个以AB为弦的弓形暗礁区域,要求轮船在行驶过程中,对两灯塔的张角不能超过 .当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于
.当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于 .
.
(1)请用直尺和圆规在图中作出△APB的外接圆 (作出图形,不写作法,保留痕迹);
(2)若此时轮船到B的距离PB为700米,已知AB=500米,求出此时轮船到A的距离.
如图,在直角坐标系中,已知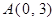 、
、 、
、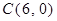 、
、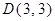 ,点P从C点出发,沿着折线C﹣D﹣A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.
,点P从C点出发,沿着折线C﹣D﹣A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.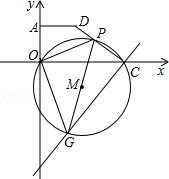
(1)直接写出∠DCO的度数;
(2)当点P在线段CD上运动时,求△OPG的最小面积;
(3)设圆心M的纵坐标为n,试探索:在点P运动的整个过程中,n的取值范围.
如图所示,已知圆锥底面半径r=10cm,母线长为40cm.
(1)求它的侧面展开图的圆心角;
(2)若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,求它所走的最短路线。
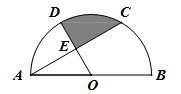
如图,点C,D是半圆O的三等分点,直径AB= .连结AC交半径OD于E,则线段DE,CE以及
.连结AC交半径OD于E,则线段DE,CE以及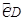 围成的封闭图形(即阴影部分)的面积是 .
围成的封闭图形(即阴影部分)的面积是 .
如图,已知☉O的直径AB=8,过A、B两点作☉O的切线AD、BC.
(1)当AD=2,BC=8时,连接OC、OD、CD.
①求△COD的面积.
②试判断直线CD与☉O的位置关系,并说明理由.
(2)若直线CD与☉O相切于点E,设AD=x(x>0),试用含x的式子表示四边形ABCD的面积S,并探索S是否存在最小值,写出探索过程.
如图1,在直角坐标系中,点A的坐标为(1,0),以OA为一边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1,且OD≠2),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.

(1)试找出图1中的一个损矩形 ;
(2)试说明(1)中找出的损矩形一定有外接圆;
(3)随着点D的位置变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由.
(4)在图2中,过点M作MG⊥y轴,垂足是点G,连结DN,若四边形DMGN为损矩形,求点D的坐标.
由“不在同一直线上的三点确定一个圆”,可以判断平面直角坐标系内的三个点A(3,0)、B(0,﹣4)、C(2,﹣3) 确定一个圆(填“能”或“不能”).
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若 ,且OC=4,求PA的长和tanD的值.
,且OC=4,求PA的长和tanD的值.
已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
(1)如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;
小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.
请你借鉴小明的方法写出AM的长,并写出推理过程.
(2)若△ABC为等腰直角三角形,∠BAC= ,
, ,
, (其中
(其中 ),直接写出AM的长(用含有a,b的代数式表示).
),直接写出AM的长(用含有a,b的代数式表示).
如图,A、B、C为⊙O上三点,∠ACB=20○,则∠BAO的度数为 ;