两圆的半径分别为2和1,圆心距为3,则反映这两圆位置关系的为图()
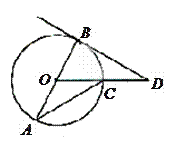
如图, 的直径
的直径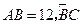 的长为2
的长为2 ,
,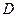 在
在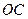 的延长线上,且
的延长线上,且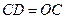 .
.
(1)求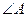 的度数;
的度数;
(2)求证: 是
是 的切线;
的切线;
(参考公式:弧长公式 ,其中
,其中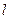 是弧长,
是弧长, 是半径,
是半径,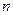 是圆心角度数)
是圆心角度数)
(10分) 如图9,已知,在△ABC中,∠ABC= ,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
(1)求证:ED是⊙O的切线.
(2)如果CF ="1,CP" =2,sinA = ,求⊙O的直径BC.
,求⊙O的直径BC.
如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD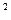 =AB·AE,求证:DE是⊙O的切线.
=AB·AE,求证:DE是⊙O的切线.

第20题图
如图,⊙O中,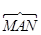 的度数为320°,则圆周角∠MAN=____________.
的度数为320°,则圆周角∠MAN=____________.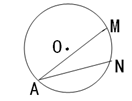
(本小题满分9分)
如图,已知⊙O1与⊙O2都过点A,AO1是⊙O2的切线,⊙O1交O1O2于点B,连结AB并延长交⊙O2于点C,连结O2C.
(1)求证:O2C⊥O1O2;
(2)证明:AB·BC=2O2B·BO1;
(3)如果AB·BC=12,O2C=4,求AO1的长.
(本题满分10分,每小题5分)
请你把上面的解答再认真地检查一遍,别留下什么遗憾,并估算一下成绩是否达到了80分,如果你的全卷得分低于80分,则本题的得分将计入全卷总分,但计入后全卷总分最多不超过80分;如果你全卷得分已经达到或超过80分,则本题的得分不计入全卷总分.
(1)计算 -2 +3的结果是_ _;
(2)如图,点C在⊙O上,∠ACB=50°,则∠AOB=_ _°
(本题满分10分,每小题5分)
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.
(1)若∠B=30°,AB=2,求CD的长;
(2)求证:AE2=EB·EC.
如图2,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为()
| A.30° | B.40° | C.50° | D.60 |
如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若 ,则
,则 的度数为
的度数为
A. |
B. |
C. |
D. |
 为
为 的直径,
的直径, 为弦,且
为弦,且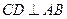 ,垂足为
,垂足为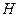 .
.
(1)如果 的半径为4,
的半径为4,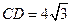 ,求
,求 的度数;
的度数;
(2)若点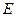 为
为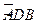 的中点,连结
的中点,连结 ,
, .求证:
.求证: 平分
平分 ;
;
(3)在(1)的条件下,圆周上到直线 距离为3的点有多少个?并说明理由.
距离为3的点有多少个?并说明理由.
如图7,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB的长度为_________cm.
同一平面内,半径分别是2cm和3cm的两圆的圆心距为5cm,则这两圆的位置关系是
| A.相离 | B.相交 | C.外切 | D.内切 |