图(四)为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与 交于另一点D。若A=70,B=60,则
交于另一点D。若A=70,B=60,则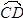 的度数为何?
的度数为何?
| A.50 | B.60 | C.100 | D.120 |
如图(二), 为圆O的直径,C、D两点均在圆上,其中
为圆O的直径,C、D两点均在圆上,其中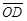 与
与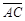 交于E点,且
交于E点,且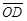 ^
^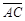 。若
。若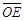 =4,
=4,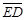 =2,则
=2,则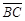 长度为何?
长度为何?
| A.6 | B.7 | C.8 | D.9 |
(本题8分)
如图,AB是⊙O的直径,C是 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD ﹦6, AC ﹦8,则⊙O的半径为 ▲,CE的长是 ▲.
如图所示,
△ABC的三个顶点的坐标分别为A(-1,3)、B (-2,-2)、C (4,-2),则△ABC外接圆半径的长度为.
(本题8分)
如图,AB是⊙O的直径,C是 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.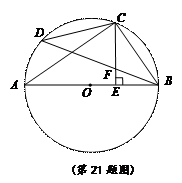
(1)求证:CF﹦BF;
(2)若CD ﹦6, AC ﹦8,则⊙O的半径为 ▲,CE的长是 ▲.
如果半径为3cm的⊙O1与半径为4cm的⊙O2内切,那么两圆的圆心距O1O2= ▲ cm.
如图,△ABC内接于⊙O,∠A=40°,则∠BOC的度数为( ▲)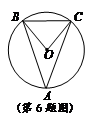
| A.20° | B. 40° | C. 60° | D.80° |
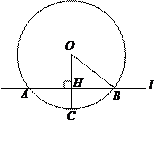
如图,直线l与⊙O相交于A,B两点,且与半径OC垂直,垂足为H ,已知AB=16厘米,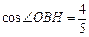 .
.
(1) 求⊙O的半径;
(2) 如果要将直线l向下平移到与⊙O相切的位置,平移的距离应是多少?请说明理由.
如图,△ABC是⊙O的内接三角形,点D是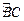 的中点,
的中点,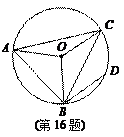
已知∠AOB=98°,∠COB=120°.则∠ABD的度数是 .
外切两圆的半径分别为2 cm和3cm,则两圆的圆心距是
| A.1cm | B.2cm | C.3cm | D.5cm |
如图,AB是⊙O的直径, P为AB延长线上任意一点,C为半圆ACB的中点,PD切⊙O于点D,连结CD交AB于点E.
求证:(1)PD=PE;
(2)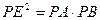 .
.
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD=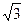 ,∠ACB=30°.
,∠ACB=30°.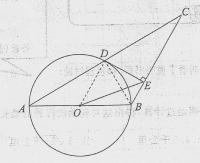
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若AB=10,CD=8,
则线段OE的长为.
如图,点A、B、C在⊙O上,若∠BAC= 24°,则∠BOC= °.