初中数学三角形的五心解答题

如图（1），AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．

（1）若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；0．com
（2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变．设点Q的运动速度为x cm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由．zx100．com

一架云梯长25 m，如图所示斜靠在一面墙上，梯子底端C离墙7 m．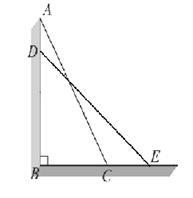

（1）这个梯子的顶端A距地面有多高？
（2）如果梯子的顶端下滑了4 m，那么梯子的底部在水平方向也是滑动了几米？

一艘轮船由于风向原因先向正东方向航行了160km，然后向正北方向航行120km，这时它离出发点有多远？

已知：如图，，，．求证：．

如图，已知AB=AC，AD=AE．求证：BD=CE．

如图，∠A=∠B，CE∥DA，CE交AB于E．求证：△CEB是等腰三角形．

如图所示，在△ABC中，AB=AC，∠C=30°，AB⊥AD，AD=4cm，求BC的长．

如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N两点，DM与EN相交于点F．

（1）若△CMN的周长为15cm，求AB的长；
（2）若∠MFN=70°，求∠MCN的度数．

如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．

求证：（1）D是BC的中点；
（2）△BEC∽△ADC；
（3）若，求⊙O的半径。

如图，某大楼的顶部树有一块广告牌CD，小明在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度，AB=10米，AE=15米．

（1）求点B距水平面AE的高度BH；
（2）求广告牌CD的高度．
（测角器的高度忽略不计，结果精确到0．1米．参考数据：）

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B．

（1）求证：△ADF∽△DEC
（2）若AB＝4，AD＝3,AE＝3,求AF的长．

已知，边长为6的等边三角形ABC,建立适当的直角坐标系，

（1）写出各个顶点的坐标．
（2）求出这个等边三角形的面积．

已知：如图，∠ACB＝∠ADB＝90°，AC＝AD，E是AB上任意一点。

（1）BC与BD相等吗？试说明理由。
（2）CE＝DE吗？为什么？

已知，如图：△ABC是等腰直角三角形，∠ABC=90°，AB=10，D为△ABC外一点，连接AD、BD，过D作DH⊥AB，垂足为H，交AC于E．

（1）若△ABD是等边三角形，求DE的长；
（2）若BD=AB，且tan∠HDB=，求DE的长．

如图，在△ABC中，AB=AC，点D是BC的中点，AB平分∠DAE，AE⊥BE，垂足为E．

（1）求证：AD=AE；
（2）若BE∥AC，试判断△ABC的形状，并说明理由．