初中数学三角形的五心试题

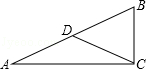
如图，已知一张长方形纸片ABCD，AB∥CD ，AD=BC=1，AB=CD=5．在长方形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK．

（1）请你动手操作，判断△MNK的形状一定是                  ；
（2）问△MNK的面积能否小于？试说明理由；
（3）如何折叠能够使△MNK的面积最大？请你用备用图探究可能出现的情况，并求最大值．

如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F．请解答下列问题：

（1）连结BD，试说明∠BDE=∠CDF；
（2）求证：BE=FC；
（2）若AE=4，FC=3，求EF长．

某航船以20海里/时的速度向正北方向航行，在A处看灯塔Q在航船北偏东45°处，半小时后航行到B处，此时灯塔Q与航船的距离最短．

（1）请你在图中画出点B的位置；
（2）求灯塔Q到A处的距离．（精确到0．1海里）

如图所示，要在公园（四边形ABCD）中建造一座音乐喷泉，喷泉位置应符合如下要求：
 
（1）到公园两个出入口A、C的距离相等；
（2）到公园两边围墙AB、AD的距离相等．
请你用尺规作图的方法确定喷泉的位置P．（不必写作法，但要保留作图痕迹）

如图，在Rt△ABC中，∠C＝90°,AC＝6,BC＝8,分别以三边为直径向上作三个半圆．

（1）AB＝      ；
（2）图中阴影部分面积＝          ．

如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为     ．

若一个等腰三角形的两边长分别为2和5，则它的周长为            ．

已知一个等腰三角形的顶角为120⁰，则它的一个底角为        度．

如图，E是BC的中点，∠1=∠2，AE=DE。

求证：AB=DC

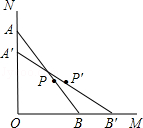
如图，一根木棒AB的长为2m斜靠在与地面垂直的墙上，与地面的倾斜角∠ABO为60°，当木棒沿墙壁向下滑动至A′，AA′=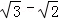，B端沿地面向右滑动至点B′，则木棒中点从P随之运动至P′所经过的路径长为（ ）

A．1

B．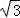

C．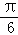

D．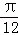

如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（4，0），B（0，3）．点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴正半轴的一动点，且满足OD=2OC，连结DE，以DE，DA为边作▱DEFA．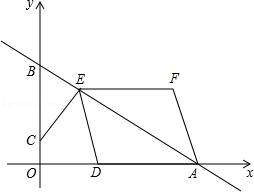

（1）当m=1时，求AE的长．
（2）当0＜m＜3时，若▱DEFA为矩形，求m的值；
（3）是否存在m的值，使得▱DEFA为菱形？若存在，直接写出m的值；若不存在，请说明理由．

已知D、E分别是△ABC的AB、AC中点，则S_△ADE：S_{四边形DBCE}=           ．

如图，在△ABC中，AD⊥CA于点A，交BC于点D，M是CD的中点，连接AM，AM=AB．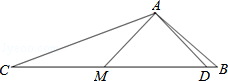

（1）求证：CD=2AB；
（2）若AC=8，AB=5，求AD的长．

已知：如图，△AOC≌△BOD．求证：△AOD≌△BOC．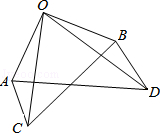

如图，在Rt△ABC中，∠C=90°，AB=10cm，D为AB的中点，则CD=      cm．