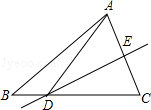
如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为 .
一个等腰三角形的一腰上的高与另一腰的夹角为40°,则它的顶角为: °.
若一个多边形的内角和为1080°,则这个多边形的边数为( )
| A.6 | B.7 | C.8 | D.9 |
如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.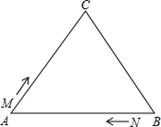
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.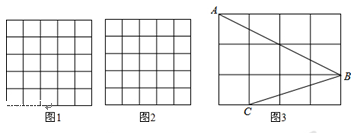
(1)在图1中以格点为顶点画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、 、
、 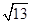 ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
如图,在△ABC中,BC边的垂直平分线交BC于D,交AB于E,若CE平分∠ACB,∠B=40°则∠A= 度.
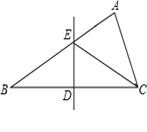
如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
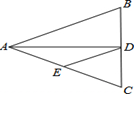
| A.20 | B.12 | C.14 | D.13 |
如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“趣味三角形”.
(1)请用尺规作图的方式,画一个“趣味三角形”(保留作图痕迹);
(2)如图,在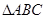 中,∠C=90°,AD是BC边上的中线,已知AC=
中,∠C=90°,AD是BC边上的中线,已知AC=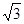 ,BC=2,请判断
,BC=2,请判断 是不是“趣味三角形”,并说明理由。
是不是“趣味三角形”,并说明理由。
已知:如图AB∥CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.求证:PA=PD.
在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为 cm2.
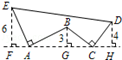
如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是 .
直角三角形两条边长分别是5和12,则第三边上的中线长是 .
已知△ABC的三边长a、b、c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是 .