初中数学一次函数的最值试题

如图1，菱形ABCD中，∠A=60°，点P从A出发，以2cm/s的速度沿边AB、BC、CD匀速运动到D终止，点Q从A与P同时出发，沿边AD匀速运动到D终止，设点P运动的时间为t（s）．△APQ的面积S（cm²）与t（s）之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出．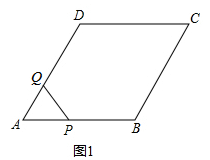
 
（1）求点Q运动的速度；
（2）求图2中线段FG的函数关系式；
（3）问：是否存在这样的t，使PQ将菱形ABCD的面积恰好分成1：5的两部分？若存在，求出这样的t的值；若不存在，请说明理由．

如图1，P（2，2），点A在x轴正半轴上运动，点B在y轴上运动，且PA=PB．

（1）求证：PA⊥PB；
（2）若点A（8，0），求点B的坐标；
（3）求OA – OB的值；
（4）如图2，若点B在y轴正半轴上运动时，直接写出OA+OB的值．

某自行车队根据队员速度的不同，分为快1组、快2组、慢1组和慢2组四个小组，在该车队的一次训练中，快1组和慢1组从甲地行进到乙地，剩下的组从乙地行进到甲地．快1组和慢1组同时从甲地出发，快1组的队员以高于慢1组队员10km/h的速度前行，快1组行驶一段时间后因某些原因又往回行驶（在往返过程中速度不变），最终与慢1组汇合，汇合后两组继续以各自的速度向乙地行进．设快1组和慢1组行驶的时间为t，与甲地的距离为s，s与t之间的函数图象如图所示．

（1）求OA解析式；
（2）已知甲地到乙地的距离为90km，在快1组与慢1组汇合时，慢2组（慢2组的速度与慢1组相同）由乙地开始出发，经过一段时间后，快1组和慢2组同时到达补给站．
①求此时慢2组与甲地之间的距离；
②若快2组在某一时刻也从乙地出发，速度与快1组相同，如果快2组不能比慢2组晚到甲地，求快2组比慢2组最多晚出发多少小时？

已知A、B两市相距260千米.甲车从A市前往B市运送物资，行驶2小时在M地汽车出现故障，立即通知技术人员乘乙车从A市赶来维修（通知时间忽略不计）.乙车到达M地后又经过20分钟修好甲车，后按原路原速返回，同时甲车以原速1.5倍的速度前往B市.如图是两车距A市的路程y (千米)与甲车行驶时间x (小时)之间的函数图象，结合图象回答下列问题：

（1）甲车提速后的速度是_______千米/小时，乙车的速度是_______千米/小时，点C的坐标为_____________.
（2）求乙车返回时y与x的函数关系式并写出自变量x的取值范围；
（3）求甲车到达B市时乙车已返回A市多长时间.

郑州市花卉种植专业户王有才承包了30亩花圃，分别种植康乃馨和玫瑰花，有关成本、销售额见下表：

种植种类	成本（万元/亩）	销售额（万元/亩）
康乃馨	2.4	3
玫瑰花	2	2.5

（1）2012年，王有才种植康乃馨20亩、玫瑰花10亩，求王有才这一年共收益多少万元？（收益=销售额-成本）
（2）2013年，王有才继续用这30亩花圃全部种植康乃馨和玫瑰花，计划投入成本不超过70万元.若每亩种植的成本、销售额与2012年相同，要获得最大收益，他应种植康乃馨和玫瑰花各多少亩？
（3）已知康乃馨每亩需要化肥500kg,玫瑰花每亩需要化肥700kg，根据（2）中的种植亩数，为了节约运输成本，实际使用的运输车辆每次装载化肥的总量是原计划每次装载总量的2倍，结果运输全部化肥比原计划减少2次.求王有才原定的运输车辆每次可装载化肥多少千克？

已知点A、B分别在一次函数y=x，y=8x，的图像上，其横坐标分别为a、b(a>0，b>O)．若直线AB为一次函数y=kx+m，的图像，则当是整数时，满足条件的整数k的值共有        个．

如图，在平面直角坐标系中，点A在y轴上，点B在x轴上，C是线段AB的中点，连接OC，并过点A作OC的垂线，垂足为D，交x轴于点E，已知tan∠OAD=．

（1）求2∠OAD的正切值；
（2）若OC=．
①求直线AB的解析式；
②求点D的坐标．

小明在一次数学兴趣小组活动中，对一个数学问题作如下探究：
问题情境：如图1，四边形ABCD中，AD∥BC，点E为DC边的中点，连结AE并延长交BC的延长线于点F．求证：S_{四边形ABCD}＝S_△ABF．（S表示面积）

问题迁移：如图2，在已知锐角∠AOB内有一定点P．过点P任意作一条直线MN，分别交射线OA、OB于点M、N．小明将直线MN绕着点P旋转的过程中发现，△MON的面积存在最小值．请问当直线MN在什么位置时，△MON的面积最小，并说明理由．

实际应用：如图3，若在道路OA、OB之间有一村庄Q发生疫情，防疫部分计划以公路OA、OB和经过防疫站的一条直线MN为隔离线，建立一个面积最小的三角形隔离区△MON．若测得∠AOB＝66º，∠POB＝30º，OP＝4km，试求△MON的面积．（结果精确到0.1km²）（参考数据：sin66º≈0.91，tan66º≈2.25，≈1.73）
拓展延伸：如图4，在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）、（6，3）、、（4，2），过点P的直线l与四边形OABC一组对边相交，将四边形OABC分成两个四边形，求其中以点O为顶点的四边形的面积的最大值．

某地为改善生态环境，积极开展植树造林，甲、乙两人从近几年的统计数据中有如下发现：

（1）求y₂与x之间的函数关系式？
（2）若上述关系不变，试计算哪一年该地公益林面积可达防护林面积的2倍？这时该地公益林的面积为多少万亩？

函数与的图象在同一平面直角坐标系内的交点的个数是（    ）

A．1个

B．2个

C．3个

D．0

如图，抛物线y=x²+mx+n交x轴于A、B两点，交y轴于点C，点P是它的顶点，点A的横坐标是-3，点B的横坐标是1．

(1)求m、n的值；
(2)求直线PC的解析式；
(3)请探究以点A为圆心、直径为5的圆与直线PC的位置关系，并说明理由．(参考数据：≈1.41，≈1.73，≈2.24)

如图，已知点A是第一象限内横坐标为的一个定点，AC⊥x轴于点M，交直线y=－x于点N．若点P是线段ON上的一个动点，∠APB=30°，BA⊥PA，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B运动的路径长是　 　．

如图，在平面直角坐标系中，点O为坐标原点，A点的坐标为(3，0)，以OA为边作等边三角形OAB，点B在第一象限，过点B作AB的垂线交x轴于点C．动点P从O点出发沿OC向C点运动，动点Q从B点出发沿BA向A点运动，P，Q两点同时出发，速度均为1个单位／秒。设运动时间为t秒．

（1）求线段BC的长；
（2）连接PQ交线段OB于点E，过点E作x轴的平行线交线段BC于点F。设线段EF的长为m，求m与t之间的函数关系式，并直接写出自变量t的取值范围：
（3）在（2）的条件下，将△BEF绕点B逆时针旋转得到△BE′F′，使点E的对应点E′落在线段AB上，点F的对应点是F′，E′F′交x轴于点G，连接PF、QG，当t为何值时，?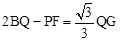

一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为x h，两车之间的距离为y km，图中的折线表示y与x之间的函数关系．根据图象解决以下问题：

（1）慢车的速度为   km/h，快车的速度为   km/h；
（2）解释图中点D的实际意义并求出点D的坐标；
（3）求快车出发多少时间时，两车之间的距离为300km？

如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数的图象交于一、三象限内的A、B两点，直线AB与x轴交于点C，点B的坐标为（﹣6，n），线段OA=5，E为x轴正半轴上一点，且tan∠AOE=

（1）求反比例函数的解析式；
（2）求△AOB的面积．