[江苏]2012-2013学年江苏省海门市八年级下学期期末考试数学试卷
如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=128°,则∠DBC的度数为
A.52° B.62° C.72° D.128°
如图,在平面直角坐标系中,平行四边形OABC的顶点为 O(0,0)、A(1,2)、B(4,0),则顶点C的坐标是 
| A.(-3,2) | B.(5,2) | C.(-4,2) | D.(3,-2) |
某小组7名同学积极参加支援“希望工程” 的捐书活动,他们捐书的册数分别是(单位:本): 10,12,10,13,10,15,17,这组数据的众数和中位数分别是
| A.10,12 | B.10,13 | C.10,10 | D.17,10 |
若矩形对角线相交所成钝角为120°,较短的边长为4cm,则对角线的长为
| A.2cm | B.4cm | C.6cm | D.8cm |
下列轴对称图形中,只用一把无刻度的直尺不能画出对称轴的是
| A.菱形 | B.矩形 | C.等腰梯形 | D.正五边形 |
如图,点P在y轴正半轴上运动,点C在x轴上运动,过点P且平行于x轴的直线分别交函数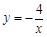 和
和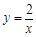 于A、B两点,则△ABC的面积等于
于A、B两点,则△ABC的面积等于
A.3 B.4 C.5 D.6
如图,在四边形ABCD中,已知AB不平行CD,∠ABD=∠ACD,请你添加一个条件: ,使得加上这个条件后能够推出AD∥BC且AB=CD. 
已知双曲线 经过点(2,3),如果A(a1,b1),B(a2,b2)两点在该双曲线上,且a1<0<a2,那么b1 b2.
经过点(2,3),如果A(a1,b1),B(a2,b2)两点在该双曲线上,且a1<0<a2,那么b1 b2.
如图,在菱形ABCD中,E、F分别是AC、CD的中点,若EF的长是2cm,则菱形ABCD的周长是 _cm. 
小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为 m.
若将7个数按照从小到大的顺序排成一列,中间的数恰是这7个数的平均数,前4个数的平均数是25,后4个数的平均数是35,则这7个数的和为 .
在直角坐标系中,已知两点A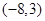 、B
、B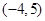 以及动点C
以及动点C 、D
、D ,则当以点A、 B、C 、D为顶点的四边形的周长最小时,比值
,则当以点A、 B、C 、D为顶点的四边形的周长最小时,比值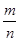 为 .
为 .
如图已知四边形ABCD是平行四边形,AC与BD相交于O点,且BC⊥AC,AB=8,∠ABC=30°,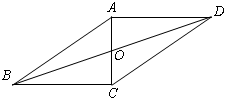
(1)求AD和BD的长;
(2)求平行四边形ABCD的面积.
某中学组织全校3200名学生进行了“法律法规”相关知识竞赛.为了解本次知识竞赛的成绩情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图.
| 分组 |
频数 |
频率 |
| 50.5~60.5 |
m |
0.05 |
| 60.5~70.5 |
a |
b |
| 70.5~80.5 |
80 |
n |
| 80.5~90.5 |
104 |
0.26 |
| 90.5~100.5 |
148 |
0.37 |
| 合计 |
|
1 |
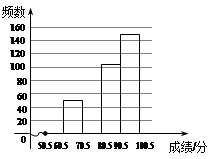
请根据以上提供的信息,解答下列问题:
(1)则a= ,b= ,并补全频数分布直方图;
(2)上述学生成绩的中位数落在哪一组范围内?
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校3 200名学生中约有多少名获奖?
某汽车油箱的容积为70升,小王把油箱注满油后准备驾驶汽车从县城到300千米外的省城接待客人,在接到客人后立即按原路返回,请回答下列问题:
(1)油箱注满油后,汽车能够行驶的总路程y(单位:千米)与平均耗油量x(单位:升/千米)之间有怎样的函数关系?
(2)如果小王以平均每千米耗油0.1升的速度驾驶汽车到达省城,在返程时由于下雨,小王降低了车速,此时每行驶1千米的耗油量增加了一倍,如果小王一直以此速度行驶,邮箱里的油是否够回到县城?如果不够用,至少还需加多少油?
如图,△ABC中,AB=AC,AD,CD分别是△ABC两个外角的平分线。
(1)求证:AC=AD;
(2)若∠B=60°,求证:四边形ABCD是菱形.
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)慢车的速度为 km/h,快车的速度为 km/h;
(2)解释图中点D的实际意义并求出点D的坐标;
(3)求快车出发多少时间时,两车之间的距离为300km?
如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(2)连接DE,当t为何值时,△DEF为直角三角形?
(3)如图②,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形 AEA′D为菱形?
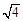 的值是
的值是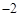
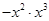 的结果是
的结果是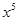
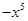
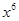



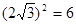
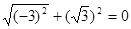
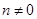 )是关于x的方程
)是关于x的方程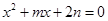 的根,则m+n的值为
的根,则m+n的值为 有意义,x的取值范围是 .
有意义,x的取值范围是 . 和
和 ,则斜边长为 .
,则斜边长为 . ;(2)
;(2)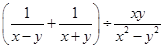 .
.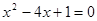 ;(2)
;(2)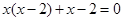 .
. 、
、
 ,求
,求 的值.
的值. 的图象上.
的图象上.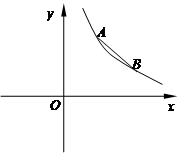
 粤公网安备 44130202000953号
粤公网安备 44130202000953号