初中数学一次函数的最值试题

如图,直线AB分别与两坐标轴交于点A（4,0）.B（0,8）,点C的坐标为（2,0）.

（1）求直线AB的解析式；
（2）在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使与相似,若存在,求出点P的坐标,若不存在,请说明理由.

如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x²－6x+8=0的两个根（OA＜OB）,点C在y轴上,且OA︰AC=2︰5,直线CD垂直于直线AB于点P,交x轴于点D.

（1）求出点A、点B的坐标.
（2）请求出直线CD的解析式.
（3）若点M为坐标平面内任意一点,在坐标平面内是否存在这样的点M,使以点B、P、D、M为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标；若不存在,请说明理由.

在平面直角坐标系xOy中，直线分别与x轴，y轴交于过点A，B，点C是第一象限内的一点，且AB=AC，AB⊥AC，抛物线经过A，C两点，与轴的另一交点为D．
（1）求此抛物线的解析式；
（2）判断直线AB与CD的位置关系，并证明你的结论；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A,B,M,N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．

如图，直线AC是一次函数y=2x+3的图象，直线BC是一次函数y=﹣2x﹣1的图象．

（1）求A、B、C三点的坐标；
（2）求△ABC的面积．

如图，直线和x轴、y轴的交点分别为B、C，点A的坐标是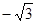（，0），另一条直线经过点A、C．

（1）求直线AC所对应的函数表达式；
（2）动点M从B出发沿BC运动，运动的速度为每秒1个单位长度．当点M运动到C点时停止运动．设M运动t秒时，△ABM的面积为S．
① 求S与t的函数关系式；
② 当t为何值时，（注：表示△ABC的面积），求出对应的t值；
③当 t=4的时候，在坐标轴上是否存在点P，使得△BMP是以BM为直角边的直角三角形？若存在，请直接写出P点坐标，若不存在，请说明理由。

（本小题满分9分）如图，直线y＝ax＋1与x轴、y轴分别相交于A、B两点，与双曲线y＝（x＞0）相交于点P，PC⊥x轴于点C，且PC=2，点A的坐标为．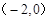

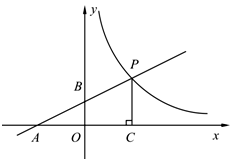
（1）求双曲线的解析式；
（2）若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q、C、H为顶点的三角形与△AOB相似时，求点Q的坐标.

（本小题满分12分）已知直线y=kx+b（k≠0）过点F（0，1），与抛物线y=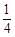x²相交于B、C两点.
（1）如图1，当点C的横坐标为1时，求直线BC的解析式；
（2）在（1）的条件下，点M是直线BC上一动点，过点M作y轴的平行线，与抛物线交于点D，是否存在这样的点M，使得以M、D、O、F为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由；
（3）如图2，设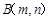（m<0），过点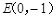的直线l∥x轴，BR⊥l于R，CS⊥l于S，连接FR、FS．试判断△RFS的形状，并说明理由．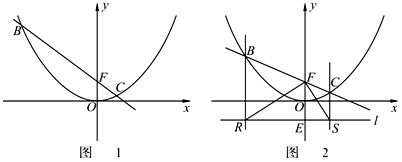

如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为底边在y轴右侧作等腰三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为    ．

已知一次函数y＝▓▓的图像过点A（0,3），B（2,4），C（m，0）题目中的阴影部分是一段因墨水污染而无法辨认的文字．
（1）根据已有的信息你能求出一次函数的表达式吗？若能，写出解题过程；不能，说明理由
（2）小明说“不用求表达式也能画出函数的图像”你认为对吗？为什么？
（3）根据表达式画出函数图像
（4）过点B能不能画一条直线将△ABO（O为坐标原点）分成面积比为1:2两部分？若能可以画几条？并写出此直线对应的函数表达式

我市高新技术开发区的某公司，用480万元购得某种产品的生产技术后，并进一步投入资金1520万元购买生产设备，进行该产品的生产加工，已知生产这种产品每件还需成本费40元．经过市场调研发现：该产品的销售单价，需定在100元到300元之间较为合理．当销售单价定为100元时，年销售量为20万件；当销售单价超过100元，但不超过200元时，每件新产品的销售价格每增加10元，年销售量将减少0.8万件；当销售单价超过200元，但不超过300元时，每件产品的销售价格在200元基础上每增加10元，年销售量将减少1万件．设销售单价为x（元），年销售量为y（万件），年获利为w（万元）．（年获利=年销售额-生产成本-投资成本）（1）直接写出y与x之间的函数关系式；
（2）求第一年的年获利w与x间的函数关系式，并说明投资的第一年，该公司是盈利还是亏损？若盈利，最大利润是多少？若亏损，最少亏损是多少？
（3）若该公司希望到第二年底，除去第一年的最大盈利（或最小亏损）后，两年的总盈利不低于1842元，请你确定此时销售单价的范围．在此情况下，要使产品销售量最大，销售单价应定为多少元？

（本题12分）某中学为筹备校庆，准备印制一批纪念册，每册由4张彩页，6张黑白页构成．印
制该纪念册的总费用由制版费和印刷费两部分组成，其中制版费的价格为：彩页300元/张，黑白页50元/
张；印刷费用与印数的关系见下表：

印数x（千册）	1≤x＜5	x≥5
彩色（元/张）	2．2	2．0
黑白（元/张）	0．7	0．6

 
（1）印制这批纪念册需制版费         元，印制1千册纪念册的印刷费           元；
（2）若印制这批纪念册共需y元，则
①当1≤x＜5时，求y关于x的函数表达式；
②当y≤60 080元，最多能印多少册？

如图：直线y=kx+3与x轴、y轴分别交于A、B两点，tan∠OAB=，点C（x，y）是直线y=kx+3上与A、B不重合的动点．

（1）求直线y=kx+3的解析式；
（2）当点C运动到什么位置时△AOC的面积是6；
（3）过点C的另一直线CD与y轴相交于D点，是否存在点C使△BCD与△AOB全等？若存在，请求出点C的坐标；若不存在，请说明理由．

某学校开展“青少年科技创新比赛”活动，“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型．甲、乙两车同时分别从A，B出发， 沿轨道到达C处，在AC上，甲的速度是乙的速度的1．5倍，设t后甲、乙两遥控车与B处的距离分别为d₁（米），d₂（米），则d₁，d₂与t的函数关系如图，试根据图象解决下列问题：

（1）填空：乙的速度v₂=_______________米/分；
（2）写出d₁与t的函数关系式；
（3）若甲乙两遥控车的距离超过10米时信号不会产生相互干扰，试探求什么时间两遥控车的信号不会产生相互干扰？

如图，已知平面直角坐标系中，直线y＝kx（k≠0）经过点（a，a）（a＞0）．线段BC的两个端点分别在x轴与直线y＝kx上（B、C均与原点O不重合）滑动，且BC＝2，分别作BP⊥x轴，CP⊥直线y＝kx，交点为P，经探究在整个滑动过程中，P、O两点间的距离为定值   ．

如图，在平面直角坐标系中，直线AB与x轴、y轴的正半轴分别交于点A，B，直线CD与x轴正半轴、y轴负半轴分别交于点D，C，AB与CD相交于点E，点A，B，C，D的坐标分别为（8，0）、（0，6）、（0，﹣3）、（4，0），点M是OB的中点，点P在直线AB上，过点P作PQ∥y轴，交直线CD于点Q，设点P的横坐标为m．
（1）求直线AB，CD对应的函数关系式；
（2）用含m的代数式表示PQ的长；
（3）若以点M，O，P，Q为顶点的四边形是矩形，请直接写出相应的m的值．