江苏省无锡市北塘区九年级第一次模拟考试数学试卷
下列计算正确的是( )
| A.(2a2)3=8a5 | B.( )2=9 )2=9 |
C.3 - - =3 =3 |
D.-a8÷a4=-a4 |
已知圆柱的底面半径为2cm,高为4cm,则圆柱的侧面积是( )
| A.16 cm2 | B.16π cm2 | C.8π cm2 | D.4π cm2 |
如图是正方体的展开图,则原正方体相对两个面上的数字之和的最大值是( )
| A.6 | B.7 | C.8 | D.9 |
假期里小菲和小琳结伴去超市买水果,三次购买的草莓价格和数量如下表:
| 价格/(元/kg) |
12 |
10 |
8 |
合计/kg |
| 小菲购买的数量/kg |
2 |
2 |
2 |
6 |
| 小琳购买的数量/kg |
1 |
2 |
3 |
6 |
从平均价格看,谁买得比较划算?( )
A.一样划算 B.小菲划算 C.小琳划算 D.无法比较
一件服装标价200元,若以6折销售,仍可获利20%,则这件服装的进价是( )
| A.100元 | B.105元 | C.108元 | D.118元 |
如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是( )
A. cm B.
cm B. cm C.
cm C. cm D.5
cm D.5 cm
cm
如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )
A.12 B.9 C.4 D.6
D.6
如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An-1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y= (x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是 ( )
(x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是 ( )
A. |
B. |
C. |
D. |
已知,如图,△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,若EG=3,则AC= .
如图,等边△ABC中,AB=4,O为三角形中心,⊙O的直径为1,现将⊙O沿某一方向平移,当它与等边△ABC的某条边相切时停止平移,记平移的距离为d ,则d的取值范围是 .
如图,已知平面直角坐标系中,直线y=kx(k≠0)经过点(a, a)(a>0).线段BC的两个端点分别在x轴与直线y=kx上(B、C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P,经探究在整个滑动过程中,P、O两点间的距离为定值 .
a)(a>0).线段BC的两个端点分别在x轴与直线y=kx上(B、C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P,经探究在整个滑动过程中,P、O两点间的距离为定值 .
(本题满分8分,每题4分)计算:
(1) +2sin45°-
+2sin45°-
(2)2(a+1)-(3-a)(3+a)-
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.
九年级学生体育模考成绩统计表
| 体育成绩 |
人数(人) |
百分比(%) |
| 26 |
|
|
| 27 |
m |
|
| 28 |
8 |
16 |
| 29 |
|
24 |
| 30 |
15 |
|

根据上面提供的信息,回答下列问题:
(1)m= ;抽取的部分学生体育模考成绩的中位数为 ;
(2)已知该校九年级共有500名学生,如果体育模考成绩达29分(含29分)为优秀,请估计该校九年级学生体育模考成绩达到优秀的总人数.
在一个盒子中装有红球、绿球、白球各1个,这3个球除颜色外其余都相同,小明先从盒子中摸出2个球后放回,小李再从盒子中摸出2个球.请用列表或画树状图法求他们摸到的4个球恰好包含所有颜色的概率.
快、慢两车分别从相距480km的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图像,结合图像解答下列问题:
(1)求慢车的行驶速度和a的值.
(2)快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)两车出发后几小时相距的路程为200千米?
如图,已知扇形AOB中,∠AOB=120°,弦AB=2 ,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M, 分别过点A、B作⊙M的切线,两切线相交于点C.
(1)求弧AB的长;
(2)试判断∠ACB的大小是否随点M的运动而改变,若不变,请求出∠ACB的大小;若改变,请说明理由.
如图1,在平面直角坐标系中,已知点A(-6,0),点B(0,8),点C在y轴上,将△OAB沿直线AC对折,使点O落在边AB上的点D处.
(1)求直线AB、AC的解析式.
(2)如图2,过B作BE⊥AC,垂足为E,若F为AB边上一动点,是否存在点F,使C为△EOF内心,若存在,请求出F点坐标,若不存在,请说明理由.
如图,已知直线y=- x+2与坐标轴交于A、B两点,抛物线y=-
x+2与坐标轴交于A、B两点,抛物线y=- +bx+c与x轴交于A、C两点,与y轴交于点B.
+bx+c与x轴交于A、C两点,与y轴交于点B.
(1)求b、c的值.
(2)平行于y轴的直线x=2交直线AB于点D,交抛物线于点E.①点P从原点O出发,沿x轴正方向以1个单位/秒的速度运动,设运动时间为t,过点P作x轴的垂线与直线AB交于点F,与抛物线交于点G,当t为何值时,FG∶DE=1∶2?②将抛物线向上平移m(m>0)个单位后与y轴相交于点B′,与直线x=2相交于点E′,当E′O平分∠B′E′D时,求m的值.
如图,已知直线l ∥l
∥l ,一个45°角的顶点A在l
,一个45°角的顶点A在l 上,过A作AD⊥l
上,过A作AD⊥l ,垂足为D,AD=6.将这个角绕顶点A旋转(角的两边足够长).
,垂足为D,AD=6.将这个角绕顶点A旋转(角的两边足够长).

(1)如图,旋转过程中,若角的两边与l 分别交于B、C,且AB=AC,求BD的长.
分别交于B、C,且AB=AC,求BD的长.
为了解决这个问题,下面提供一种解题思路:如图,作∠DAP=45°,AP与l 相交于点P,过点C作CQ⊥AP于点Q.∵∠DAP=∠BAC =45°,∴∠BAD=∠CAQ, 请你接下去完成解答.
相交于点P,过点C作CQ⊥AP于点Q.∵∠DAP=∠BAC =45°,∴∠BAD=∠CAQ, 请你接下去完成解答.
(2)旋转过程中,若角的两边与l 分别交于E、F(E在F左面),且AE>AF,DF= 2,求DE的长.请你借鉴(1)的做法在备用图中画图并解答这个问题.
分别交于E、F(E在F左面),且AE>AF,DF= 2,求DE的长.请你借鉴(1)的做法在备用图中画图并解答这个问题.
 的值等于( )
的值等于( )

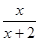 中自变量x的取值范围是 .
中自变量x的取值范围是 .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号