快、慢两车分别从相距480km的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图像,结合图像解答下列问题: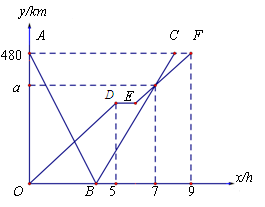
(1)求慢车的行驶速度和a的值.
(2)快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)两车出发后几小时相距的路程为200千米?
相关知识点
推荐套卷

 中,
中,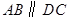 ,
,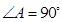 ,
,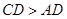 ,将纸片沿过点
,将纸片沿过点 的直线折叠,使点
的直线折叠,使点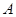 落在边
落在边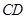 上的点
上的点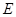 处,折痕为
处,折痕为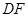 .连接
.连接 并展开纸片.
并展开纸片. 是正方形;
是正方形;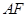 的中点
的中点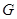 ,连接
,连接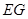 ,如果
,如果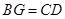 ,试说明四边形
,试说明四边形 是等腰梯形.
是等腰梯形.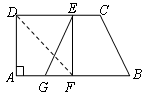
 -4)÷
-4)÷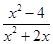 ,当
,当 满足
满足 ,且x为正整数时,求代数式的值.
,且x为正整数时,求代数式的值.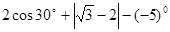 ;(2)解方程
;(2)解方程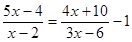 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号