如图，已知平面直角坐标系中，直线y＝kx（k≠0）经过点（a，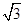
a）（a＞0）．线段BC的两个端点分别在x轴与直线y＝kx上（B、C均与原点O不重合）滑动，且BC＝2，分别作BP⊥x轴，CP⊥直线y＝kx，交点为P，经探究在整个滑动过程中，P、O两点间的距离为定值 ．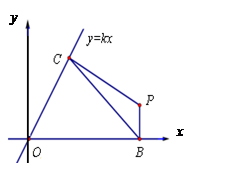
相关试题
，则点P的坐标为___ ___.
）
的图象经过点（1，－2），那么k 的值等于 ．相关知识点
推荐套卷
如图，已知平面直角坐标系中，直线y＝kx（k≠0）经过点（a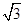，a）（a＞0）．线段BC的两个端点分别在x轴与直线y＝kx上（B、C均与原点O不重合）滑动，且BC＝2，分别作BP⊥x轴，CP⊥直线y＝kx，交点为P，经探究在整个滑动过程中，P、O两点间的距离为定值 ．
粤公网安备 44130202000953号