一次函数y=6x+1的图象不经过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(本小题满分9分)已知A、B两地的路程为240千米,某经销商每天都要用汽
车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和
火车中的一种进行运输,且须提前预订.。现在有货运收费项目及收费标准表,行驶路程S
(千米)与行驶时间t(时)的函数图象(如图13中①),上周货运量折线统计图(如图13
中②)等信息如下:


(1)汽车的速度为__________千米/时,火车的速度为_________千米/时;
(2)设每天用汽车和火车运输的总费用分别为y汽(元)和y火(元),分别求y汽、y火与x的函数关系式(不必写出x的取值范围)及x为何值时y汽>y火;(总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前下周预定哪种运输工具,才能使每天的运输总费用较省?
一次函数y=3x-2的函数值y随自变量x值的增大而_____________(填“增大”或“减小”).
(本小题满分8分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印 刷费两部分,乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.
刷费两部分,乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.
(1) 请你直接写出甲厂的制版费及y甲与x的函数解析式,并求出其证书印刷单价.
(2) 当印制证书8千个时,应选择哪个印刷厂节省费用,节省费用多少元?

 (3) 如果甲厂想把8千个证书的印制工作承揽下来,在不降低制版费的前提下,每个证书最少降
(3) 如果甲厂想把8千个证书的印制工作承揽下来,在不降低制版费的前提下,每个证书最少降 低多少元?
低多少元?
某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题:
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
某公司生产的一种时令商品每件成本为20元,经过市场调研发现,这种商品在未来20天内的日销售量m(件)与时间t(天)的关系如表:
| 时间t(天) |
1 |
3 |
6 |
10 |
… |
| 日销售量m(件) |
94 |
90 |
84 |
76 |
… |
未来20天内每天的价格y(元/件)与时间t(天)的函数关系式为y= t+25(1≤t≤20且t为整数).
t+25(1≤t≤20且t为整数).
(1)认真分析表中的数据,用所学过的函数知识,确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)设未来20天日销售利润为p(元).请求出p(元)与t(天)之间的关系式;并预测未来20天中哪一天的日销售利润最大,最大日销售利润是多少?
函数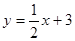 的图象与x、y轴分别交于点A、B,点P
的图象与x、y轴分别交于点A、B,点P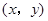 为直线AB上的一动点(
为直线AB上的一动点(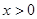 )过P作PC
)过P作PC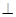 y轴于点C,若使
y轴于点C,若使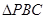 的面积大于
的面积大于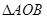 的面积,则P的横坐标x的取值范围是( )
的面积,则P的横坐标x的取值范围是( )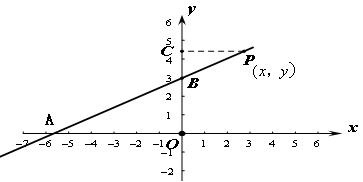
A、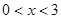 B、
B、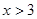 C、
C、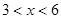 D、
D、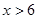
如图,在平面直角坐标系xOy中,我把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(﹣1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.
(1)求两条射线AE,BF所在直线的距离;
(2)当一次函数y=x+b的图象与图形C恰好只有一个公共点时,写出b的取值范围;
当一次函数y=x+b的图象与图形C恰好只有两个公共点时,写出b的取值范围;
(3)已知▱AMPQ(四个顶点A,M,P,Q按顺时针方向排列)的各顶点都在图形C上,且不都在两条射线上,求点M的横坐标x的取值范围.
小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),若小亮上坡、平路、下坡的速度分别为v1,v2,v3,v1<v2<v3,则小亮同学骑车上学时,离家的路程s与所用时间t的函数关系图象可能是( )
A. |
B. |
C. |
D. |
如图,直线l: ,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).
,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).
已知:关于x的一元二次方程mx2﹣(4m+1)x+3m+3="0" (m>1).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2(其中x1>x2),若y是关于m的函数,且y=x1﹣3x2,求这个函数的解析式;
(3)将(2)中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当关于m的函数y=2m+b的图象与此图象有两个公共点时,b的取值范围.
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为 ,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
| A.3 | B.4 | C.5 | D.6 |
如图,已知直线y=x+4与两坐标轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是 .
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).
(1)已知点A(﹣ ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线y= x+3上的一个动点,
x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标.
在平面直角坐标系中,直线l:y=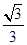 x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是( )
x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是( )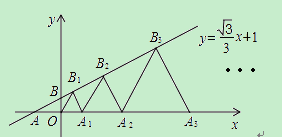
A.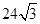 |
B.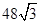 |
C.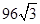 |
D.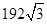 |