福建省福鼎市十校联合八年级下学期期中考试数学试卷
已知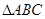 的三边长分别是6cm、8cm、10cm,则
的三边长分别是6cm、8cm、10cm,则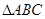 的面积是( )
的面积是( )
A.24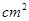 |
B.30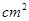 |
C.40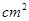 |
D.48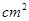 |
如图,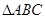 中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB、BC于点D、E,则
中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB、BC于点D、E,则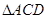 的周长( )cm
的周长( )cm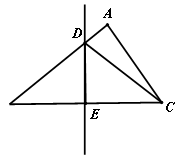
A、 6 B、 7 C、 8 D、9
在直角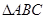 纸片中,已知
纸片中,已知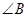 =
=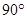 ,AB=6,,BC=8,折叠纸片使AB边与AC边重合,B点落在点E上,折痕为AD,则BD的长为( )
,AB=6,,BC=8,折叠纸片使AB边与AC边重合,B点落在点E上,折痕为AD,则BD的长为( ) 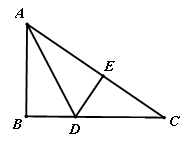
| A.3 | B.4 | C.5 | D.6 |
函数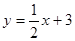 的图象与x、y轴分别交于点A、B,点P
的图象与x、y轴分别交于点A、B,点P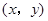 为直线AB上的一动点(
为直线AB上的一动点(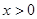 )过P作PC
)过P作PC y轴于点C,若使
y轴于点C,若使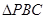 的面积大于
的面积大于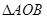 的面积,则P的横坐标x的取值范围是( )
的面积,则P的横坐标x的取值范围是( )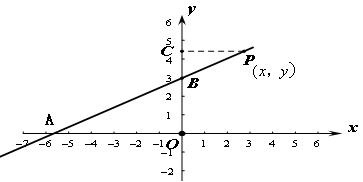
A、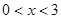 B、
B、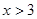 C、
C、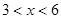 D、
D、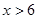
如图,△ABC中,∠C=90°,∠A=30°,BD平分∠CBA交AC于点D,若CD=2cm,则AD= cm。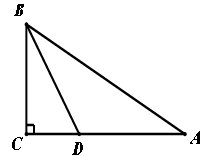
如图,在△ABC和△DEF中,已知:AC=DF,,BC=EF,要使△ABC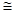 △DEF,还需要的条件可以是 ;(只填写一个条件)
△DEF,还需要的条件可以是 ;(只填写一个条件)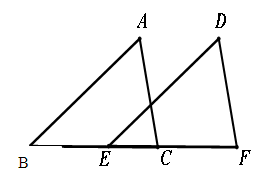
如图,点P是 ∠AOB的角平分线上一点,过点P作PC⊥OA于点C,且PC=3,则点P到OB的距离等于 ;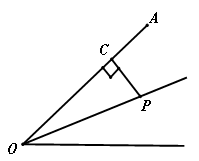
△ABC中,AB=BC,∠A=40°,点D为AC边上任意一点(不与点A、C重合),当△BCD为等腰三角形时,∠ABD的度数是 ;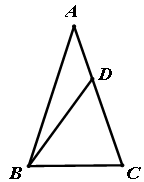
如图,∠A=∠D=90°,AC=BD,
(1)求证:AB=CD
(2)请判断△OBC的形状,并说明理由。
如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3),
(1)、画出△ABC向右平移三个单位的对应图形△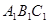 ,并写出
,并写出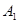 的坐标;
的坐标;
(2)、画出△ABC关于原点O对称的△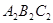 ,并写出
,并写出 的坐标;
的坐标;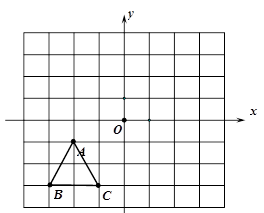
暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人1000元的两家旅行社。经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按7折收费;乙旅行社的优惠条件是:学生、家长都按8折收费。假设这两位家长带领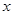 名学生去旅行,甲、乙旅行社的收费分别为
名学生去旅行,甲、乙旅行社的收费分别为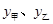 ,
,
(1)、写出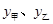 与
与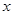 的函数关系式。
的函数关系式。
(2)、学生人数在什么情况下,选择甲旅行社更省钱?
甲、乙两人骑车前往A地,他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)、甲、乙两人的速度各是多少?
(2)、求甲距A地的路程S与行驶时间t的函数关系式。
(3)、直接写出在什么时间段内乙比甲距离A 地更近?(用不等式表示)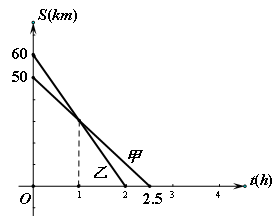
情境·观察:
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△ ,如图1所示,将△
,如图1所示,将△ 的顶点
的顶点 与点A重合,并绕点A按逆时针方向旋转,使点D,A(
与点A重合,并绕点A按逆时针方向旋转,使点D,A( ),B在同一条直线上,如图2所示,观察图2可知:旋转角
),B在同一条直线上,如图2所示,观察图2可知:旋转角 = ° ,与BC相等的线段是 。
= ° ,与BC相等的线段是 。
问题·探究:
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰直角△ABE和等腰直角△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,试探究EP与FQ之间的数量关系,并证明你的结论。
关系·拓展:
如图4,已知正方形ABCD,P为边BC上任意一点,连结AP,把AP绕点P顺时针方向旋转90°,点A对应点为点 ,连接
,连接 ,求
,求 的度数。
的度数。
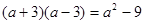
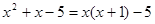
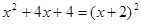
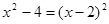
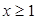 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )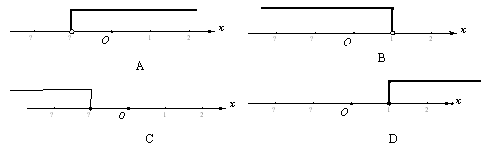
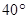 ,则它的底角是( )
,则它的底角是( )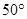
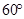

 按逆时针方向旋转900后的图形是( )
按逆时针方向旋转900后的图形是( )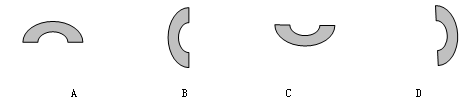
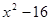 的结果是( )
的结果是( )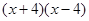
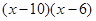
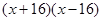
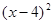
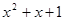
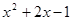
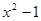
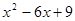
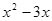 = ;
= ;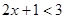 的解集是 ;
的解集是 ;
 (2)、
(2)、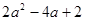
 ,并把解集在数轴上表示出来
,并把解集在数轴上表示出来 粤公网安备 44130202000953号
粤公网安备 44130202000953号