初中数学一次函数的最值填空题

如图，已知函数和的图象交于点P，则根据图象可得，关于的二元一次方程组的解是________________。

点A（1，m）在函数的图像上，则点A关于y轴的对称点的坐标是_________．

已知正比例函数的图像经过点（2，-6），则这个函数的解析式为__________。

某水库的水位在5小时内持续上涨，初始水位高度为6米，水位以每小时0.3米的速度匀速上升， 则水库的水位与上涨时间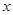之间的函数关系式是      .

已知一次函数的图像经过点A（0,2）和点B（2，－2）：（1）求出y关于x的函数表达式为         ；（2）当－2＜y＜4时，x的取值范围是             ．

在平面直角坐标系中,一次函数的图像与函数（＞0）的图像相交于点A,B,设点A的坐标为（,）,那么长为,宽为的矩形的面积为      ,周长为   

如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为底边在y轴右侧作等腰三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为    ．

已知直线与x轴、y轴分别交于A、B两点，点C（0，n）是y轴上一点，把坐标平面沿直线AC折叠，使点B刚好落在x轴上，则点C的坐标是_________________．

如图，第一象限内的点在反比例函数的图象上，第二象限内的点在反比例函数的图象上，且，，则的值为       ．

如图，直线与，轴分别交于，两点，以为边在轴右侧作等边，将点向左平移，使其对应点恰好落在直线上，则点的坐标为      ．

一次函数y=kx+b与y=-x+1平行,且经过点（6,4）,则表达式为：             .

如果直线y=-2x+b与两坐标轴所围成的三角形面积是9，则b的值为_____．

一次函数经过点（–1 , 2）且y随x增大而减小，写出一个满足条件的函数关系式_____.

、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛，比赛开始时乙在起点，甲在乙的前面，他们同时出发，匀速前进，已知甲的速度为15m/s，设甲、乙两人之间的距离为y（米），比赛时间为x（秒），图中的折线表示从两人出发至乙先到达终点的过程中y （米）与x（秒）的函数关系，根据图中信息，乙到终点时， 甲离终点还有           米．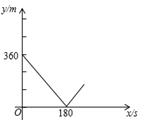

在平面直角坐标系中，记直线为．点是直线与轴的交点，以为边做正方形,使点落在在轴正半轴上，作射线交直线于点，以 为边作正方形,使点落在在轴正半轴上，依次作下去，得到如图所示的图形．则点的坐标是         ，点的坐标是     ．