初中数学一次函数的最值填空题

某书定价25元，如果一次购买20本以上，超过20本的部分打八折，试写出付款金额y（单位：元）与购书数量x（单位：本）之间的函数关系          ．

观察如图象，你认为ax＞bx+c的解集应该是      ．

已知一次函数y=kx+k﹣4的图象经过点（1，2），则k的值为      ．

某种灯的使用寿命为1000小时，它的可使用天数与平均每天使用的小时数之间的函数关系式为            ．

函数和的图象相交于点A（，3），则不等式的解集为               ．                     

如图，直角坐标系中，点P（t，0）是x轴上的一个动点，过点P作y轴的平行线，分别与直线y=x，直线y=﹣x交于A，B两点，以AB为边向右侧作正方形ABCD．

（1）当t=2时，正方形ABCD的周长是            ．
（2）当点（2，0）在正方形ABCD内部时（不包括边上），t的取值范围是                 ．

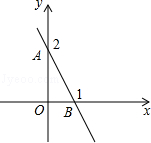
如图，一次函数y=kx+b的图象经过点A（0，2），点B（1，0），则不等式kx+b＜0的解集为      ．

已知y与x成正比例，且当x=1时，y=0.5，则y与x的函数关系式是      ．

将直线y=3x+1平移向下平移4个单位，则平移后的解析式为      ．

若点P（﹣1，m）是y=﹣x+1与y=kx+5的交点，则k的值是      ．

已知一次函数y=kx+b，当0≤x≤2时，对应的函数值y的取值范围是﹣2≤y≤4，则kb的值为      ．

某人用面值50元的IC卡从A地向B地打长途电话，按通话时间收费，3min内收费2.4元，以后每超过1min加收1元．若此人第一次通话tmin（3≤t≤45），则IC卡的余额y（元）与通话时间t（min）之间的关系式是      ．

函数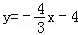的图象交x轴于A，交y轴于B，则AB两点间的距离为      ．

一次函数的图象过点（﹣1，0），且函数值随着自变量的增大而减小，写出一个符合这个条件的一次函数解析式：      ．（答案不唯一）

函数y=2x﹣4与y=3x﹣3的图象的交点坐标是      ．