初中数学一次函数的最值解答题

如图1所示，某乘客乘高速列车从甲地经过乙地到丙地，列车匀速行驶，图2为列车离乙地路程y（千米）与行驶时间x（小时）时间的函数关系图象．

（1）填空：甲、丙两地距离        千米．
（2）求高速列车离乙地的路程y与行驶时间x之间的函数关系式，并写出x的取值范围．

某超市对进货价为10元/千克的某种苹果的销售情况进行统计，发现每天销售量y（千克）与销售价x（元/千克）存在一次函数关系，如图所示．

（1）求y关于x的函数关系式（不要求写出x的取值范围）；
（2）应怎样确定销售价，使该品种苹果的每天销售利润最大？最大利润是多少？

（本题8分）在平面直角坐标系中，直线y=kx﹣2经过点A（﹣2，0），求不等式kx+3≤0的解集．

【实际情境】
某中学九年级学生步行到郊外春游．一班的学生组成前队，速度为4km/h，二班的学生组成后队，速度为6km/h．前队出发1h后，后队才出发，同时，后队派一名联络员骑自行车在两队之间不间断地来回进行联络，他骑车的速度为12km/h．
【数学研究】
若不计队伍的长度，如图，折线A-B-C、A-D-E分别表示后队、联络员在行进过程中，离前队的路程y（km）与后队行进时间x（h）之间的部分函数图象．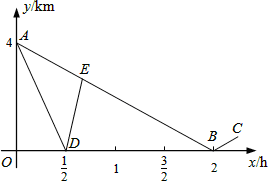

（1）求线段AB对应的函数关系式；
（2）求点E的坐标，并说明它的实际意义；
（3）联络员从出发到他折返后第一次与后队相遇的过程中，当x为何值时，他离前队的路程与他离后队的路程相等？

随着信息技术的快速发展，“互联网+”渗透到我们日常生活的各个领域，网上在线学习交流已不再是梦，现有某教学网站策划了A，B两种上网学习的月收费方式：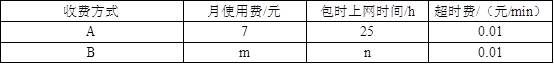

设每月上网学习时间为x小时，方案A，B的收费金额分别为，．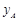
（1）如图是与x之间函数关系的图象，请根据图象填空：m=       ；n=       ；

（2）写出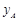与x之间的函数关系式．
（3）选择哪种方式上网学习合算，为什么？

已知：如图1，在△ABC中，A、B、C的坐标分别为（1,0），（4,0），（0,2），点M为边BC上的中点，点N为边AB 上一点，且N的横坐标为方程2n^２＋5n－12＝0一个根，
（1）求N的坐标和直线MN的解析式 ；（3+3）
（2）判断直线MN与BC的位置关系，并说明你的理由；（1+3）
（3）如图2，①在图2中作出△ABC的外接圆；②过Q（，0）作直线⊥x轴，点P在直线上，且在第一象限，试确定一个点P，使得∠CPB+∠CAB=180°，求出满足条件的P点坐标．

某商场欲购进果汁饮料和碳酸饮料共50箱，果汁饮料毎箱进价为55元，售价为63元；碳酸饮料毎箱进价为36元，售价为42元；设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注，总利润=总售价﹣总进价），
（1）设商场购进碳酸饮料y箱，直接写出y与x的函数关系式；
（2）求总利润w关于x的函数关系式；
（3）如果购进两种饮料的总费用不超过2000元，那么该商场如何进货才能获利最多？并求出最大利润．

某商场购进一批单价为4元的日用品．若按每件5元的价格销售，每月能卖出300件；若按每件6元的价格销售，每月能卖出200件，假定每月销售件数y（件）与价格x（元/件）之间满足一次函数关系．
（1）试求y与x之间的函数关系式；
（2）当销售价格定为多少时，才能使每月的利润最大？每月的最大利润是多少？

如图，在平面直角坐标系中，一次函数y=2x+b的图象与反比例函数y=（k≠0）的图象交于A、B两点，与x轴交于点C（-2，0），点A的坐标为（n，6）．

（1）求该反比例函数的解析式；
（2）求点B的坐标，写出正比例函数值大于反比例函数值时自变量x的取值范围；
（3）若点E为x轴上使△ACE为直角三角形的一点，求点E的坐标．

为奖励在演讲比赛中获奖的同学，班主任派学习委员小明为获奖同学买奖品，要求每人一件．小明到文具店看了商品后，决定奖品在钢笔和笔记本中选择．如果买4个笔记本和2支钢笔，则需86元；如果买3个笔记本和1支钢笔，则需57元．
（1）求购买每个笔记本和钢笔分别为多少元？
（2）售货员提示，买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受8折优惠，若买x（x＞0）支钢笔需要花y元，请你求出y与x的函数关系式；
（3）在（2）的条件下，小明决定买同一种奖品，数量超过10个，请帮小明判断买哪种奖品省钱．

为加强公民的节水意识，合理利用水资源．某市对居民用水实行阶梯水价，居民家庭每月用水量划分为三个阶梯，一、二、三级阶梯用水的单价之比等于1：1.5：2．如图折线表示实行阶梯水价后每月水费 $y$（元）与用水量 $x$m³之间的函数关系．其中线段AB表示第二级阶梯时 $y$与 $x$之间的函数关系.

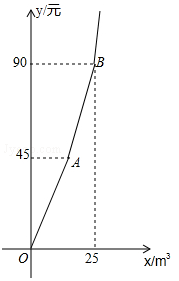
（1）写出点 $B$的实际意义；
（2）求线段 $AB$所在直线的表达式；
（3）某户5月份按照阶梯水价应缴水费102元，其相应用水量为多少立方米？

某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按120个工时计算）生产空调器、彩电、冰箱共360台，且冰箱至少生产60台，已知生产这些家电产品每台所需工时和每台产值如下表：

家电名称	空调	彩电	冰箱
工 时	1 2	1 3	1 4
产值（千元）	4	3	2

 
问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？（以千元为单位）

开学初，小明到文具批发部一次性购买某种笔记本，该文具批发部规定：这种笔记本售价y（元/本）与购买数量x（本）之间的函数关系如图所示．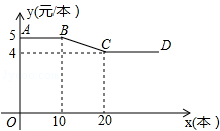

（1）图中线段AB所表示的实际意义是     ；
（2）请直接写出y与x之间的函数关系式；
（3）已知该文具批发部这种笔记本的进价是3元/本，若小明购买此种笔记本超过10本但不超过20本，那么小明购买多少本时，该文具批发部在这次买卖中所获的利润W（元）最大？最大利润是多少？

如图，一次函数y＝x＋6与反比例函数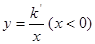的图象相交于A，B两点，与x轴、y轴交于E、F，点B的横坐标为。

（1）试确定反比例函数的解析式；
（2）求点E、F的坐标。

在奉贤创建文明城区的活动中，有两段长度相等的彩色道砖铺设任务，分别交给甲、乙两个施工队同时进行施工．如图是反映所铺设彩色道砖的长度y（米）与施工时间x（时）之间关系的部分图象．请解答下列问题：

（1）求乙队在2≤x≤6的时段内，y与x之间的函数关系式；
（2）如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到12米/时，结果两队同时完成了任务．求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米？