已知：如图1，在△ABC中，A、B、C的坐标分别为（1,0），（4,0），（0,2），点M为边BC上的中点，点N为边AB 上一点，且N的横坐标为方程2n２＋5n－12＝0一个根，
（1）求N的坐标和直线MN的解析式 ；（3+3）
（2）判断直线MN与BC的位置关系，并说明你的理由；（1+3）
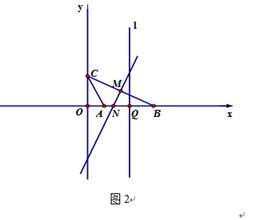
（3）如图2，①在图2中作出△ABC的外接圆；②过Q（
，0）作直线
⊥x轴，点P在直线上，且在第一象限，试确定一个点P，使得∠CPB+∠CAB=180°，求出满足条件的P点坐标．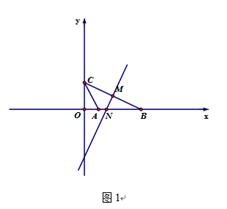
相关试题
会产生增根，求m的值。
，其中x为不等式组
的整数解．
=
RtΔABC中，∠C=90°，点D、E分别是ΔABC边AC、BC上的点，点P是一动点.令∠PDA=∠1，∠PEB=∠2，∠DPE=∠
.
（1）若点P在线段AB上，如图（1）所示，且∠=50°，则∠1+∠2=___________°；
（2）若点P在边AB上运动，如图（2）所示，则∠、∠1、∠2之间有何关系？
（3）若点P在Rt△ABC斜边BA的延长线上运动（CE＜CD），则∠、∠1、∠2之间有何关系？猜想并说明理由。
相关知识点
推荐套卷
粤公网安备 44130202000953号